第五章数据资产定价的参考模型：人类视角

5.1 数据资产定价的理论基础

数据资产定价需要建立在坚实的理论基础之上，同时考虑数据的特殊属性。本节将从传统资产定价理论出发，结合前文建立的数据价值理论，构建数据资产定价的基础框架。

5.1.1 传统资产定价理论回顾

金融资产定价模型概述

传统金融资产定价主要基于以下模型：

资本资产定价模型(CAPM)： $$E(R_i) = R_f + \beta_i[E(R_m) - R_f]$$ 其中 $R_f$ 是无风险收益率，$\beta_i$ 是系统性风险系数。
套利定价理论(APT)： $$E(R_i) = R_f + \sum_{j=1}^n \beta_{ij}\lambda_j$$ 其中 $\lambda_j$ 是风险因子溢价，$\beta_{ij}$ 是敏感度系数。

传统定价模型的局限性

在应用于数据资产时，传统模型存在以下局限：

收益的不确定性：数据资产的收益难以准确预测
风险度量的困难：传统的$\beta$系数难以应用
市场完备性缺失：数据资产市场尚不完善
价值传递机制差异：数据使用不遵循传统的稀缺性原则

数据资产定价的特殊性

数据资产具有独特的定价特征：

非竞争性：多方可同时使用
价值递增性：使用不会损耗，可能增值
场景依赖性：价值随使用场景变化
网络外部性：价值受整体数据生态影响

5.1.2 数据价值与信息价值的映射关系

价值映射函数的构造

基于前文的理论框架，构建价值映射函数：

$$V_A(D) = \phi(V_I(F(D))) + \int_{\mathcal{M}} \rho(D,m)dm$$

其中：

$V_A(D)$ 是数据资产价值
$V_I(F(D))$ 是信息价值
$\phi$ 是价值转换函数
$\rho(D,m)$ 代表市场状态变量。

信息熵与价值度量

引入信息熵作为基础价值度量：

$$V_{base}(D) = \alpha H(D) + \beta I(D;Y)$$

其中：

$H(D)$ 是数据的信息熵
$I(D;Y)$ 是与目标变量的互信息
$\alpha, \beta$ 是权重系数

时间维度的价值演化

考虑时间因素的价值演化：

$$V(D,t) = V_{\text{info}}(D)e^{-\lambda t} + \int_0^t g(s)e^{-\lambda(t-s)}ds$$

其中：

$\lambda$ 是基础价值衰减率
$g(s)$ 是价值生成函数
$r$ 是时间折现率

5.1.3 数据资产的价值组成

基础信息价值

基础信息价值由数据的内在特性决定：

$$V_{info}(D) = \sum_{i=1}^n w_i m_i(D)$$

其中：

$m_i(D)$ 是各种信息特征度量
$w_i$ 是对应权重

使用价值与潜在价值

使用价值考虑实际应用场景：

$$V_{use}(D) = \sum_{j=1}^k p_j U_j(D)$$

潜在价值考虑未来可能性：

$$V_{potential}(D) = \mathbb{E}[\sum_{t=1}^T \gamma^t V_{future}(D,t)]$$

协同价值与网络效应

考虑数据组合产生的额外价值：

$$V_{synergy}(D_1,D_2) = V(D_1 \cup D_2) - V(D_1) - V(D_2)$$

网络效应通过规模函数体现：

$$V_{network}(D) = V_{base}(D) \cdot (1 + \eta(N))$$

其中 $\eta(N)$ 是网络规模效应函数。

这些理论基础为构建数据资产定价模型提供了必要的数学工具和概念框架。特别是，通过将传统金融理论与数据特有的价值特征相结合，我们可以建立更适合数据资产的定价模型。

5.2 数据资产定价模型的构建

基于前文建立的理论框架，我们现在构建一个完整的数据资产定价模型。这个模型需要同时考虑数据的内在价值特征和市场交易特性。

5.2.1 基础定价框架

价值评估基准

基础定价框架采用多层次结构：

$$P(D,t) = V_{base}(D,t) \cdot \gamma(t) \cdot \delta(r)$$

其中基础价值由三个核心组件构成：

$$V_{base}(D,t) = V_{info}(D) + V_{use}(D,t) + V_{potential}(D,t)$$

(a) 信息价值组件： $$V_{info}(D) = \alpha H(D) + \beta I(D;Y) + \sum_{i=1}^n w_i m_i(D)$$

$H(D)$：数据的信息熵
$I(D;Y)$：与目标变量的互信息
$m_i(D)$：其他信息特征度量

(b) 使用价值组件： $$V_{use}(D,t) = \sum_{j=1}^k p_j(t)U_j(D) \cdot (1 + \eta(N_t))$$

$U_j(D)$：不同使用场景的价值函数
$p_j(t)$：场景权重
$\eta(N_t)$：网络效应函数

时间折现机制

引入多因素时间折现机制：

$$\gamma(t) = e^{-(\lambda_1 + \lambda_2(t) + \lambda_3(m_t))t}$$

其中：

$\lambda_1$：基础时间折现率
$\lambda_2(t)$：时变折现率函数
$\lambda_3(m_t)$：市场状态相关的折现率
$m_t$：市场状态向量

时间价值调整满足：

$$\frac{\partial \gamma(t)}{\partial t} = -(\lambda_1 + \lambda_2’(t) + \lambda_3’(m_t)\frac{\partial m_t}{\partial t})\gamma(t)$$

风险调整因子

风险调整采用多维度方法：

$$\delta(r) = \exp(-\sum_{i=1}^m \beta_i r_i)$$

其中风险因子 $r_i$ 包括：

数据质量风险
使用权限风险
市场流动性风险
技术可用性风险

风险系数 $\beta_i$ 通过以下优化问题确定：

$$\min_{\beta} \mathbb{E}[(P_{observed} - P_{model})^2] \text{ s.t. } \sum_i \beta_i = 1$$

5.2.2 多维度价值集成

信息维度的价值量化

扩展信息价值度量框架：

$$V_{info}^*(D) = V_{info}(D) + \int_{\mathcal{X}} \omega(x)I(D;X=x)dx$$

其中：

$\omega(x)$：信息价值权重函数
$I(D;X=x)$：条件互信息

引入信息完备性度量：

$$C(D) = \frac{H(D|Y)}{H(D)} \cdot \frac{I(D;Y)}{\max_{D’} I(D’;Y)}$$

使用场景的价值贡献

场景价值集成模型：

$$V_{scene}(D) = \sum_{s \in \mathcal{S}} \pi_s(t) \cdot V_s(D) \cdot (1 + \sigma_s(D))$$

其中：

$\pi_s(t)$：场景权重函数
$V_s(D)$：单场景价值函数
$\sigma_s(D)$：场景协同效应函数

场景间的价值传递：

$$\frac{\partial V_s(D)}{\partial t} = \sum_{s’ \in \mathcal{S}} k_{ss’}\frac{\partial V_{s’}(D)}{\partial t}$$

市场环境的影响因素

市场影响函数：

$$M(D,t) = \mu(t) \cdot \prod_{i=1}^k (1 + \theta_i(m_i(t)))$$

其中：

$\mu(t)$：基础市场调整因子
$\theta_i$：市场因子影响函数
$m_i(t)$：市场指标

5.2.3 动态定价机制

价值更新机制

价值动态演化方程：

$$\frac{dP(D,t)}{dt} = \alpha(t)[\hat{P}(D,t) - P(D,t)] + \sigma(t)dW_t$$

其中：

$\hat{P}(D,t)$：目标价格
$\alpha(t)$：调整速度
$\sigma(t)$：波动率
$W_t$：维纳过程

市场反馈调整

引入市场反馈机制：

$$\hat{P}(D,t) = P(D,t) + \kappa(t)\sum_{i=1}^n w_i(t)[P_i^{obs}(t) - P_i^{model}(t)]$$

其中：

$\kappa(t)$：学习率函数
$w_i(t)$：观察权重
$P_i^{obs}$：市场观察价格
$P_i^{model}$：模型预测价格

价格发现过程

价格发现通过迭代过程实现：

$$P_{t+1} = P_t + \eta_t \nabla L(P_t)$$

其中损失函数为：

$$L(P) = |P - V_{base}|^2 + \lambda_1 R_{market}(P) + \lambda_2 R_{smooth}(P)$$

$R_{market}$：市场一致性正则项
$R_{smooth}$：平滑性正则项
$\lambda_1, \lambda_2$：正则化参数

最终的定价模型通过以下优化问题求解：

$$P^*(D,t) = \arg\min_P \mathbb{E}[L(P)] \text{ s.t. } \text{Constraints}$$

其中约束条件包括：

价格非负性
市场一致性
时间连续性
价值保持性

这个完整的定价框架既保持了理论的严谨性，又提供了实践的可操作性。通过多维度的价值集成和动态调整机制，模型能够较好地捕捉数据资产的特殊属性和市场特征。

5.3 定价模型的参数估计

基于前节构建的定��模型框架，我们需要对模型中的各类参数进行科学估计。这些参数的准确性直接影响模型的有效性。

5.3.1 基础参数的确定

信息熵的计算方法

对于数据集 $D$，信息熵的计算需要考虑数据的多个维度：

(a) 离散型数据： $$H(D) = -\sum_{i=1}^n p_i \log p_i$$ 其中概率估计采用： $$p_i = \frac{count(x_i) + \alpha}{\sum_{j=1}^n count(x_j) + \alpha n}$$ 这里 $\alpha$ 是拉普拉斯平滑参数。

(b) 连续型数据： $$H(D) \approx -\int_{\mathcal{X}} f(x)\log f(x)dx \approx -\sum_{i=1}^m \hat{f}(x_i)\log \hat{f}(x_i)\Delta x$$ 其中 $\hat{f}(x)$ 通过核密度估计获得： $$\hat{f}(x) = \frac{1}{nh}\sum_{i=1}^n K(\frac{x-x_i}{h})$$

时间折现率的估计

时间折现率包含多个组件：

$$\lambda_{total}(t) = \lambda_{base} + \lambda_{time}(t) + \lambda_{market}(m_t)$$

(a) 基础折现率估计： $$\lambda_{base} = r_f + \beta_D\sigma_D$$ 其中：

$r_f$ 是无风险利率
$\beta_D$ 是数据特征系数
$\sigma_D$ 是数据价值波动率

(b) 时变折现率函数： $$\lambda_{time}(t) = a\cdot e^{-bt} + c$$ 参数通过历史数据拟合： $$\min_{a,b,c} \sum_{t=1}^T [\lambda_{obs}(t) - \lambda_{time}(t)]^2$$

风险系数的校准

风险调整因子的参数校准：

$$\delta(r) = \exp(-\sum_{i=1}^m \beta_i r_i)$$

通过最大似然估计： $$\mathcal{L}(\beta) = \sum_{t=1}^T \log p(P_t|D_t,\beta)$$

风险系数约束： $$\sum_{i=1}^m \beta_i = 1, \beta_i \geq 0$$

5.3.2 市场参数的估计

市场需求弹性

需求弹性估计模型：

$$\epsilon_D = -\frac{\partial \log Q}{\partial \log P} = -\frac{P}{Q}\frac{\partial Q}{\partial P}$$

通过回归模型估计： $$\log Q_t = \alpha - \epsilon_D \log P_t + \sum_{k=1}^K \gamma_k X_{kt} + \eta_t$$

其中：

$Q_t$ 是需求量
$P_t$ 是价格
$X_{kt}$ 是控制变量
$\eta_t$ 是误差项

竞争环境影响

竞争影响函数：

$$C(D,t) = \exp(-\sum_{j=1}^n w_j d(D,D_j))$$

其中：

$d(D,D_j)$ 是与竞争数据的距离度量
$w_j$ 是竞争者权重

竞争强度指数： $$I_{comp}(t) = \sum_{j=1}^n \pi_j(t)\cdot s_j(t)$$ 其中：

$\pi_j(t)$ 是竞争者市场份额
$s_j(t)$ 是相似度系数

宏观经济因素

宏观调整函数：

$$M(t) = \prod_{i=1}^k (1 + \theta_i E_i(t))$$

参数估计： $$\theta_i = \arg\min_{\theta} \sum_{t=1}^T [P_t - P_t^{model}(\theta)]^2$$

其中 $E_i(t)$ 包括：

GDP增长率
通货膨胀率
行业景气指数
技术发展指数

5.3.3 场景参数的评估

使用场景价值系数

场景价值函数：

$$V_s(D) = \kappa_s \cdot U_s(D) \cdot (1 + \gamma_s N_s)$$

参数估计方法： $$\kappa_s = \frac{\sum_{t=1}^T R_{st}}{\sum_{t=1}^T U_s(D_t)}$$

场景权重更新： $$\pi_s(t+1) = \pi_s(t) + \eta[\frac{R_s(t)}{R_{total}(t)} - \pi_s(t)]$$

协同效应参数

协同价值函数：

$$S(D_1,D_2) = \alpha_{12}\sqrt{V(D_1)V(D_2)}\cdot I(D_1;D_2)$$

参数估计： $$\alpha_{12} = \arg\max_{\alpha} \mathcal{L}(V_{obs}|V_{model}(\alpha))$$

协同系数矩阵： $$\Sigma = [\sigma_{ij}]{n\times n}, \sigma{ij} = \text{corr}(V(D_i),V(D_j))$$

网络外部性测度

网络效应函数：

$$\eta(N) = \begin{cases} a\log(1+bN), & N \leq N^* \ c + d\sqrt{N}, & N > N^* \end{cases}$$

参数估计通过分段回归： $$\min_{a,b,c,d,N^*} \sum_{t=1}^T [V_{obs}(t) - V_{base}(t)(1+\eta(N_t))]^2$$

网络价值乘数： $$\mu(N) = 1 + \eta(N) + \lambda\frac{d\eta(N)}{dN}$$

这些参数估计方法构成了完整的参数确定体系，它们共同支持定价模型的实际应用。特别注意：

参数估计需要考虑数据的可获得性
估计方法需要保持统计稳健性
参数更新机制需要具备适应性
不同参数之间的相关性需要考虑
估计结果需要进行有效性验证

5.4 模型的应用与验证

在建立了完整的定价模型和参数估计方法后，我们需要通过实际应用来验证模型的有效性，并基于实践经验进行持续优化。

5.4.1 典型场景应用

结构化数据定价

对于结构化数据，定价模型具体化为：

$$P_{struct}(D,t) = V_{base}(D)\cdot Q(D)\cdot T(t)\cdot M(t)$$

其中基础价值计算： $$V_{base}(D) = \sum_{i=1}^n w_i\cdot q_i\cdot v_i$$

$q_i$：数据质量指标
$v_i$：字段价值权重
$w_i$：业务重要性系数

质量调整因子： $$Q(D) = \prod_{j=1}^k (1 + \alpha_j q_j(D))$$

其中 $q_j(D)$ 包括：

完整性：$q_c = \frac{N_{valid}}{N_{total}}$
准确性：$q_a = 1 - \frac{N_{error}}{N_{total}}$
时效性：$q_t = e^{-\lambda(t-t_0)}$

非结构化数据定价

非结构化数据定价模型：

$$P_{unstruct}(D,t) = V_{content}(D)\cdot V_{format}(D)\cdot E(t)$$

内容价值评估： $$V_{content}(D) = \beta_1 H(D) + \beta_2 I(D;Y) + \beta_3 S(D)$$

其中：

$H(D)$：信息熵
$I(D;Y)$：目标相关性
$S(D)$：语义丰富度

格式价值评估： $$V_{format}(D) = \sum_{k=1}^m \gamma_k F_k(D)$$

实时数据流定价

实时数据流采用动态定价模型：

$$P_{stream}(D,t) = r(t)\cdot V(D,t)\cdot (1 + \delta(t))$$

实时价值函数： $$V(D,t) = \int_{t-\tau}^t v(D,s)e^{-\lambda(t-s)}ds$$

流量调整因子： $$r(t) = r_0(1 + \alpha\frac{dN(t)}{dt})$$

其中：

$v(D,s)$：瞬时价值函数
$N(t)$：累计数据量
$\delta(t)$：市场波动调整

5.4.2 模型的有效性验证

理论一致性检验

价值一致性验证： $$|V_{model}(D) - V_{theory}(D)| \leq \epsilon_v$$

单调性检验： $$D_1 \preceq D_2 \Rightarrow P(D_1,t) \leq P(D_2,t)$$

时间一致性： $$\frac{\partial P(D,t)}{\partial t} = -\lambda P(D,t) + f(t)$$

实证效果分析

模型性能度量： $$MSE = \frac{1}{T}\sum_{t=1}^T (P_t^{obs} - P_t^{model})^2$$

预测能力评估： $$R^2 = 1 - \frac{\sum_t (P_t^{obs} - P_t^{model})^2}{\sum_t (P_t^{obs} - \bar{P}^{obs})^2}$$

稳健性检验： $$\sigma_{model} = \sqrt{\frac{1}{T-1}\sum_{t=1}^T (P_t^{model} - \bar{P}^{model})^2}$$

市场反馈验证

市场接受度： $$A(t) = \frac{N_{accepted}(t)}{N_{total}(t)}$$

价格发现效率： $$E(t) = 1 - \frac{\text{Var}(P_t^{market} - P_t^{model})}{\text{Var}(P_t^{market})}$$

交易量响应： $$Q(t) = Q_0e^{-\eta|P_t^{market} - P_t^{model}|}$$

5.4.3 模型的优化与调整

参数动态更新

参数更新方程： $$\theta_{t+1} = \theta_t + \alpha_t\nabla L(\theta_t)$$

学习率调整： $$\alpha_t = \frac{\alpha_0}{1 + \beta t}$$

更新频率控制： $$f_{update} = \min{f_0, \frac{1}{\sigma_{\theta}^2}}$$

模型适应性改进

自适应机制： $$P_{adaptive}(D,t) = P_{base}(D,t)\cdot [1 + \phi(e_t)]$$

其中误差函数： $$e_t = P_t^{market} - P_t^{model}$$

修正函数： $$\phi(e) = \begin{cases} ke, & |e| \leq \epsilon \ \text{sign}(e)\cdot(\epsilon + \log|e/\epsilon|), & |e| > \epsilon \end{cases}$$

实践经验反馈

反馈整合机制： $$F(t) = \sum_{i=1}^n w_i(t)f_i(t)$$

权重更新： $$w_i(t+1) = w_i(t) + \eta[r_i(t) - \bar{r}(t)]$$

模型调整指标： $$I_{adjust}(t) = \begin{cases} 1, & \text{if } |F(t)| > \tau \ 0, & \text{otherwise} \end{cases}$$

实践应用中需要特别注意：

场景适应性

不同类型数据的特征提取
场景特定参数的调整
应用约束的考虑

验证全面性

多维度的效果评估
长期稳定性的验证
异常情况的处理

优化持续性

定期的模型评估
及时的参数更新
动态的策略调整

这个应用与验证框架确保了定价模型在实践中的有效性和可靠性，同时通过持续的优化和调整保持模型的适用性。

实验1 实验上述模型模拟计算模拟数据资产的总价值，考虑了信息熵、互信息、质量评分、使用价值、潜在价值等因素。

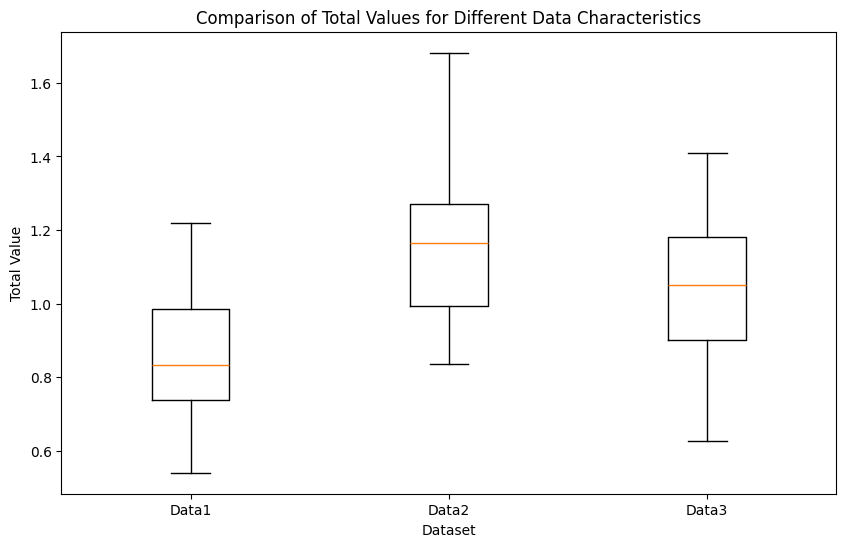
实验2 特征影响比较目标: 评估不同数据特征（如信息熵、互信息、质量评分等）对数据资产总价值的影响。步骤: 创建不同特征的数据集: 生成多个数据集，每个数据集的某个特征有显著差异。 2. 计算总价值: 使用模型计算每个数据集的总价值。 3. 比较结果: 分析不同特征对总价值的影响。

Keyboard shortcuts

数据资产定价导论