封面

前言

2019年10月18日，笔者写了一篇名为《数据有价：数据资产定价研究初探》的文章。在文章中，笔者提出“数据必然的成为可进行交易的商品、必不可少的生产要素与资产。数据资产列入资产负债表，也只是时间问题。” 随后不久的十九届四中全会首次提出将数据作为新的生产要素。2020年4月，中共中央、国务院发布《关于构建更加完善的要素市场化配置体制机制的意见》，数据作为一种新生产要素首次写入了中央文件中。自此，国内关于数据要素的研究与实践如火如荼的开展起来。

这本书正是笔者过去五年在数据资产定价领域摸索和探索的阶段性总结。随着数据作为新型生产要素的重要性日益凸显，如何科学、合理地为数据资产定价，成为了一个亟待解决的核心问题。

撰写这本书的初衷，主要源于当前数据资产领域中许多基础性的研究尚未得到充分的厘清。例如，数据资产的价值评估标准、定价模型的构建、交易机制的完善等方面，都存在着理论和实践上的空白。笔者希望通过对这些问题的系统梳理和深入探讨，为同行提供一些思路和参考。

当然，由于个人见解和能力所限，书中难免有不完善之处。在此，笔者以抛砖引玉的心态，希望能够引起学界和业界对数据资产定价问题的更多关注和讨论，共同推动这一领域的理论创新和实践发展。

张家林 2024年11月

第一章 数据流形和数据拓扑

理解数据的内在价值是数据资产定价的起点。数据的内在价值是由其本身的内在结构决定的。数据流形和数据拓扑揭示了数据的内在结构和潜在模式。通过分析数据在流形上的分布，我们能够理解数据的本质特征和局部关联性；而通过研究数据的拓扑特征，我们可以把握数据的全局结构和稳定性质。这种多维度的分析对于评估数据的价值至关重要。

数据流形的研究使我们可以量化数据的复杂性、稀缺性和实用性，而数据拓扑分析则帮助我们识别数据的持久特征、结构稳定性和全局模式。这两种方法相辅相成，共同为数据资产的定价提供科学依据。数据流形揭示了数据的几何特征和局部结构，而拓扑分析则捕捉了数据在不同尺度下的本质形态，这些都是评估数据价值不可或缺的维度。

只有同时深入了解数据的流形结构和拓扑特征，才能全面准确地评估数据资产的潜在价值和市场前景，为数据交易和投资决策奠定坚实的基础。数据的几何特征和拓扑性质共同构成了数据价值评估的理论基石，为数据资产的科学定价提供了完整的分析框架。

本章简要的介绍数据流形和数据拓扑的基本概念。

1. 什么是流形(manifold)

在数学中，流形是一个在局部看来像平坦空间的对象，但从整体上可能具有不同的形状或弯曲度。简单地说，流形就是每个小区域看起来像普通的欧几里得空间（比如直线、平面），但当这些小区域组合在一起时，整体可能呈现出更复杂的结构。

举个生活中的例子，地球表面就是一个流形。虽然地球整体是球形的，但当我们站在地面上时，周围的一小片区域看起来是平坦的。这就是为什么我们可以在小范围内使用平面地图进行导航。

流形的严格数学定义：

一个拓扑空间 $M$ 被称为 $n$ 维流形，如果满足以下条件：

1. $M$ 是豪斯多夫空间，即对于 $M$ 中的任意两点，存在不相交的开集将其分开。
2. $M$ 满足第二可数公理，即 $M$ 的拓扑基是可数的。
3. 对于 $M$ 中的每个点 $p$，存在一个开邻域 $U_p \subset M$ 和一个开集 $V_p \subset \mathbb{R}^n$，以及一个同胚映射： $$ \phi_p: U_p \rightarrow V_p $$ 使得 $\phi_p$ 是从 $U_p$ 到 $V_p$ 的同胚。

符号表示：

• 对于所有 $p \in M$，存在开集 $U_p$ 和 $V_p$，以及同胚映射 $\phi_p: U_p \rightarrow V_p \subset \mathbb{R}^n$。

如下是Klein瓶的示意图。Klein是一个二维流形，示意图显示的是klein浸入在三维空间中的情况。

关于流形的主要数学定律：

1. 维数定理： 流形的每一点都有一个确定的维数，称为其维数（dimension）。对于 $n$ 维流形，每个点的邻域都同胚于欧氏空间 $\mathbb{R}^n$。

例子： 圆周 $S^1$： 一维流形的典型例子是单位圆 $S^1$。虽然嵌入在二维平面内，但对于圆周上的每个点，其邻域都与实数轴 $\mathbb{R}^1$ 同胚。这说明了圆周是一个一维流形，每个小区域看起来都是线性的。

2. 嵌入定理（惠特尼嵌入定理）： 任意光滑的 $n$ 维流形都可以光滑嵌入到欧氏空间 $\mathbb{R}^{2n}$ 中。即存在一个光滑的单射嵌入映射： $$ f: M \hookrightarrow \mathbb{R}^{2n} $$

例子： 克莱因瓶： 克莱因瓶是一个非定向的二维流形，无法在三维空间中无自交地嵌入。然而，根据惠特尼嵌入定理，它可以嵌入到四维空间 $\mathbb{R}^4$ 中而不产生自交。这表明了高维空间中流形嵌入的可能性。

3. 子流形定理： 流形的子集在满足一定条件下也构成流形，称为子流形（submanifold）。具体来说，如果映射的秩在某点处达到最大值，那么该点就是子流形的一部分。

例子： 球面上的赤道： 三维欧氏空间中的单位球面 $S^2$ 是一个二维流形。球面上的赤道是一个一维子流形，相当于一个嵌入在 $S^2$ 中的圆周。赤道的每个点都有一个与 $\mathbb{R}^1$ 同胚的邻域。

4. 切空间与切丛： 在流形的每一点，都可以定义一个与之关联的切空间（tangent space），集合所有的切空间构成流形的切丛（tangent bundle）。切空间是流形在某点处的线性近似。

例子： 山峰上的切空间： 想象一座山的山顶，登山者站在顶点。此时，山顶处的切空间是一个与地平面平行的平面，表示登山者在该点沿各个方向移动的可能性。整个山体的切丛则包含了山体每个点的切空间的集合。

5. 斯托克斯定理： 将微积分的基本定理推广到流形上，连接了微分形式的外微分与流形的边界积分。对于流形 $M$ 和定义在其上的 $(k-1)$ 阶微分形式 $\omega$，有： $$ \int_M d\omega = \int_{\partial M} \omega $$

例子： 电磁学中的麦克斯韦方程组： 斯托克斯定理在电磁学中应用广泛。例如，安培环路定律描述了磁场沿闭合曲线的环量与通过该曲线的电流之间的关系： $$ \oint_C \mathbf{B} \cdot d\mathbf{l} = \mu_0 I $$ 这实际上是斯托克斯定理的直接应用，将曲线上的积分转换为曲面上的积分。

6. 高斯-博内定理： 将流形的几何性质与拓扑性质联系起来。对于紧致、二维的黎曼流形 $M$，其总曲率与欧拉示性数满足： $$ \int_M K , dA = 2\pi \chi(M) $$ 其中，$K$ 是高斯曲率，$\chi(M)$ 是欧拉示性数。

例子： 多面体的总曲率： 对于一个凸多面体，如正四面体，其总高斯曲率可通过各顶点的角缺损计算，并满足高斯-博内定理。总曲率与该多面体的欧拉示性数之间存在固定关系。

7. 帕拉塔-斯迈尔定理： 给出了流形间微分同胚的存在条件，是微分拓扑中的重要结果。

例子： 高维球面的同胚性： 在高维拓扑学中，该定理帮助我们理解不同维度的球面之间何时存在微分同胚。这对于分类高维流形和理解它们的结构至关重要。

2. 流形假设（Manifold Hypothesis）

流形假设是机器学习和数据科学领域的一个重要概念，用于解释高维数据的内在结构。该假设认为，高维数据实际上集中在一个隐含的、比原始空间维度低得多的流形上。换句话说，虽然数据存在于高维空间中，但其本质上由少数几个自由变量或参数所决定，因此可以近似地用低维流形来描述。

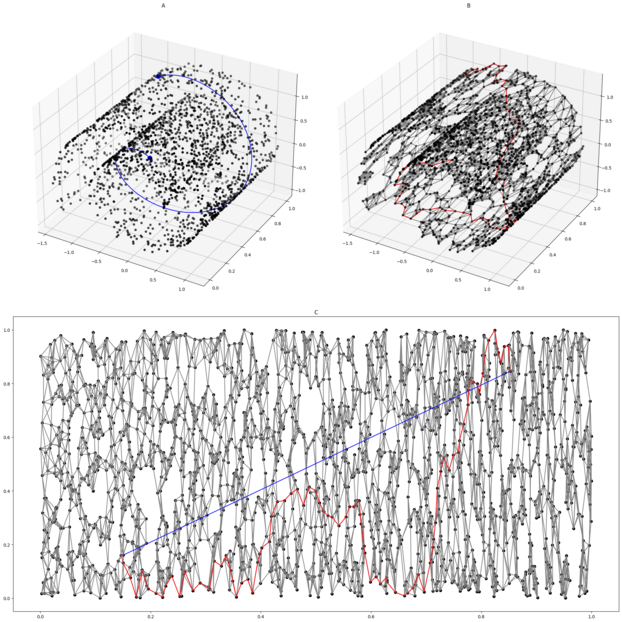
流形假设的动机

现实世界中，很多高维数据都是由一些潜在的、低维的生成过程引起的。例如：

• 图像数据：一幅图像可能包含数以万计的像素点（高维数据），但这些像素的取值往往由场景中的物体、光照、视角等少数因素决定。
• 语音信号：语音数据可以看作是高维的时间序列信号，但实际由发声器官的状态（如声带、舌头、嘴唇的位置）等低维因素控制。
• 文本数据：一篇文章可以被表示为高维的词向量，但其主题、情感等少数特征起到了主导作用。

流形假设的形式化描述

设有一个高维空间 $\mathbb{R}^D$，其中 $D$ 表示数据的观测维度。流形假设认为，数据 $X \subset \mathbb{R}^D$ 实际上被限制在一个内在维度为 $d$（$d \ll D$）的流形 $\mathcal{M}$ 上，即：

$$ X \approx \mathcal{M}, \quad \mathcal{M} \subset \mathbb{R}^D, \quad \text{dim}(\mathcal{M}) = d $$

这个流形 $\mathcal{M}$ 可以被视为一个嵌入在高维空间中的低维曲面。数据点可以通过一个从低维参数空间到高维观测空间的映射函数 $\phi$ 来生成：

$$ \mathbf{x} = \phi(\mathbf{z}), \quad \mathbf{z} \in \mathbb{R}^d $$

其中，$\mathbf{z}$ 是潜在的低维表示，$\phi$ 是一个光滑的非线性函数。

流形假设的意义

• 降维：既然数据主要位于低维流形上，那么通过降维技术，可以有效地表示和处理数据，减少计算复杂度和存储需求。
• 特征提取：流形学习方法旨在发现数据的内在结构，提取有意义的低维特征，增强模型的泛化能力。
• 数据可视化：通过将高维数据映射到二维或三维空间，可以更直观地观察数据的分布和聚类特性。

这张图片展示了不同物体在特征空间中的流形结构，以及不同类别在高维空间中如何分布。使用流形假说的概念，这些不同的物体类别（例如“vase”、“head cabbage”、“birdhouse”）可以看作高维空间中的流形，它们各自形成了具有特定形状和方向的区域。每个类别的流形代表了该类别物体在视觉特征空间中的连续分布。

图中的平面分隔了这些流形，表示一个决策边界，用于将不同类别区分开。每个类别流形中的点则代表了具体的物体样本。流形的形状反映了类别内特征的变化，例如某一类物体在形状或颜色上的差异。通过流形假说，我们可以解释为这些不同类别在高维空间中有着连续而非离散的特征分布，而分类模型的任务就是找到一个适当的分隔面，以区分这些流形。

支持流形假设的证据

• 实验观察：在很多实际数据集上，降维技术如主成分分析（PCA）能够以少数几个主成分解释大部分数据方差，表明数据确实集中在低维子空间或流形上。
• 成功的应用：流形学习方法（如Isomap、LLE、t-SNE）在图像、语音、文本等领域取得了成功，进一步支持了流形假设的有效性。

流形假设的局限性

• 复杂流形结构：某些数据的流形结构可能非常复杂，存在自相交、边界等问题，增加了学习难度。
• 噪声和测量误差：现实数据往往受到噪声影响，导致数据偏离理想的流形，影响流形学习的效果。
• 维度诅咒：尽管流形维度较低，但在高维空间中，流形仍可能呈现出高复杂度，处理和计算上依然具有挑战性。

流形假设的局限性实例

虽然流形假设在很多情况下是有用的，但是它在处理某些类型的数据时也存在局限性。例如，对于一些高度复杂和无规则性的高维数据，数据点可能并不集中在一个低维的光滑流形上。

实例：高维噪声数据

考虑一个高维空间中的随机噪声数据集。设想我们有一个由独立同分布的随机变量构成的高维数据集，其中每个维度的数据都随机且彼此独立。在这种情况下：

• 数据分布特性：数据点在高维空间中均匀分布，不存在任何内在的低维结构或模式。
• 流形学习的困难：由于数据没有低维流形结构，任何尝试将数据降维到较低维度的流形学习方法都会丢失大量信息，无法捕获数据的本质特征。
• 降维效果不佳：降维后的数据可能无法保留原始数据的统计特性，导致在后续的任务（如分类、聚类）中表现不佳。

这个实例展示了当数据本身不满足流形假设，即数据并非集中在低维流形上时，流形学习方法的局限性。在处理纯随机噪声数据或具有高度复杂性的分布时，流形假设并不适用，依赖于该假设的算法可能无法有效地分析和处理数据。

流形假设并非适用于所有类型的数据。在面对高度非结构化或复杂的数据集时，需要谨慎考虑流形假设的适用性，并选择合适的数据分析和建模方法。

3. 数据流形（Data Manifold）

数据流形的概念是流形假设在数据科学领域的具体应用。数据流形是指数据在高维空间中分布所形成的低维光滑流形结构。虽然数据存在于高维空间，但由于数据内部的关联性和约束，实际有效的自由度可能远小于表观维度。这意味着数据点实际上被限制在高维空间中的一个低维流形上。

举例来说，人脸图像识别是数据流形理论在实际应用中的典型例子。尽管每幅人脸图像在数字化后会形成一个高维空间中的点（例如，一个 $100 \times 100$ 像素的灰度图像可以表示为10,000维的向量），但人脸的变化实际上由有限的因素控制，这些因素包括：

1. 表情变化（Expression）：微笑、哭泣、惊讶等不同的面部表情导致的肌肉形变。
2. 头部姿态（Pose）：头部的转动、倾斜和俯仰等不同角度。
3. 光照条件（Illumination）：光源方向、强度和数量的变化导致的明暗差异。
4. 年龄变化（Age）：随着年龄增长带来的面部特征变化。
5. 遮挡（Occlusion）：如眼镜、帽子、头发等对面部的部分遮挡。

这些因素可以视为控制人脸图像变化的参数，其组合形成了一个低维的参数空间。在高维的像素空间中，人脸图像的数据点被限制在由这些参数空间映射得到的低维流形上。

利用数据流形的概念，可以采用各种流形学习方法来处理和分析人脸图像数据。例如：

• 局部线性嵌入（Locally Linear Embedding, LLE）：通过保持数据局部邻域的线性关系，将高维人脸数据降至低维空间，揭示其内在的流形结构。
• 等距映射（Isomap）：基于保持数据点之间的测地距离，实现高维到低维的降维过程，保留数据的全局几何特征。
• 拉普拉斯特征映射（Laplacian Eigenmaps）：利用拉普拉斯矩阵的谱分解，捕获数据流形的局部和全局结构信息。

这些方法的应用可以带来多种益处：

• 提高识别准确率：在低维流形空间中，人脸数据的类别区分更加明显，有助于提升人脸识别算法的性能。
• 降噪与特征提取：通过流形学习，可以有效地去除高维数据中的噪声，提取对识别任务最有用的特征。
• 数据可视化：将高维人脸数据映射到二维或三维空间，便于直观地观察和分析数据的分布和聚类情况。

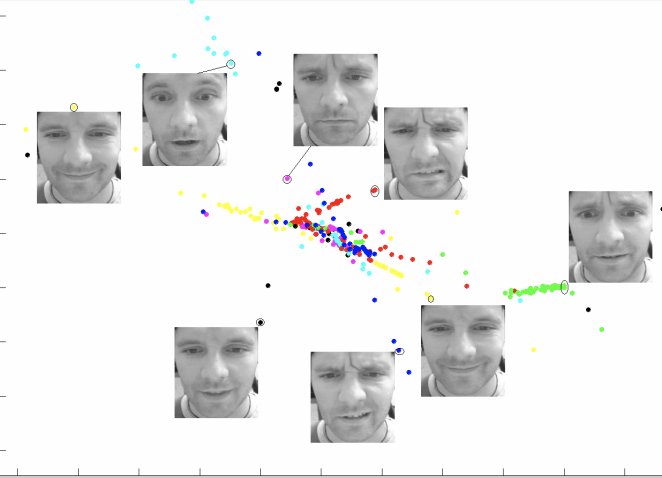
这张图片展示了人脸图像在高维特征空间中的流形结构。图中的每个散点代表一张人脸图片，通过降维技术（如 t-SNE 或 PCA）将其嵌入到二维平面上。相似的表情（如微笑、皱眉）聚集在一起，形成局部连续的流形结构，表明这些表情在高维空间中是相邻的。不同表情之间的距离则表明它们在特征空间中的差异性。因此，这张图显示了表情特征如何在高维空间中“流动”，形成一个自然的、连续的分布，从而揭示了人脸数据的内在几何结构。

3.1 深度学习

**深度学习（Deep Learning）**是一种基于人工神经网络的机器学习方法，特别是使用多层神经元网络结构来学习数据的表征和特征。它模拟人脑的神经元连接方式，通过层层抽象，从原始数据中自动提取高级特征，从而实现对复杂数据的分析和处理。

近年来，深度学习在多个领域取得了显著的成就：

• 计算机视觉：在图像分类、目标检测、图像分割、人脸识别等任务中，深度学习模型如卷积神经网络（CNN）已经超越了传统方法的性能。例如，ResNet、DenseNet等模型在ImageNet等大型数据集上取得了接近人类水平的识别准确率。

• 自然语言处理：在机器翻译、文本生成、情感分析等任务中，循环神经网络（RNN）、长短期记忆网络（LSTM）、Transformer等模型推动了技术进步。特别是BERT、GPT系列模型的出现，使得机器生成的文本更加流畅和符合语义。

• 语音识别与合成：深度学习技术使得语音识别的准确率大幅提升，并实现了高质量的语音合成，应用于智能助手、语音输入等领域。

• 游戏AI与强化学习：通过深度强化学习，AlphaGo、AlphaZero等模型在围棋、国际象棋中击败了顶尖的人类选手，展示了人工智能在复杂决策中的潜力。

深度学习之所以能够取得如此成功，关键原因在于：

1. 丰富的数据内在规律：实际世界的数据往往蕴含着复杂且有价值的模式和结构，例如图像中的边缘、纹理，语言中的语法、语义。这些内在规律为模型的学习提供了基础。

2. 强大的特征学习能力：深度学习模型具有自动提取特征的能力，不再依赖人工设计特征。多层网络结构能够从低级特征（如像素、单词）逐步抽象出高级特征（如物体、句子意义），有效捕获数据的内在规律。

3. 大量的数据和计算资源：大规模的数据集和高性能计算资源（如GPU、TPU）的可用性，使得训练深层神经网络成为可能，模型能够在海量数据中学习到更精细的模式。

4. 先进的算法与结构：如卷积神经网络、循环神经网络、注意力机制等模型结构的提出，极大地增强了模型对特定类型数据的处理能力。此外，优化算法的改进（如Adam优化器）、正则化方法（如Dropout）等也提升了模型的性能。

深度学习取得如此重大成功的关键一点是数据本身蕴含的丰富内在规律，深度学习技术能够有效地揭示并利用这些规律。

3.2 数据科学中的基本假设

在深度学习中，流形假设起着至关重要的作用。深度神经网络通过多层非线性变换，试图捕获数据的内在结构，将高维数据映射到低维流形表示。每一层网络都在提取数据的特征，将数据逐步投影到更能体现其本质的表示空间中。

基于流形假设，数据科学中的两个基本假设可以被总结出来：

1. 流形分布定律：同一类别的高维数据往往集中在某个低维流形附近。这意味着，在数据空间中，同类数据不是随机分布的，而是聚集在具有相似特征的区域内。深度学习模型通过学习这些区域，可以有效地对数据进行分类和预测。

2. 聚类分布定律：不同类别的数据对应于流形上的不同区域，这些区域之间的距离足够大，使得不同类别的数据可以被清晰地区分开来。这表明，数据在流形上的分布呈现出天然的聚类结构。深度学习通过识别和利用这些聚类结构，增强了模型的判别能力。

流形假设提供了理解高维数据结构的视角，深度学习模型则通过复杂的网络结构和学习算法，将这一假设转化为实际的数据处理能力。凭借对流形分布和聚类分布的充分利用，深度学习在图像识别、语音处理、自然语言处理等领域取得了卓越的成果。

3.3 深度学习的几何解释

深度学习中的流形映射与微分几何解释

在深度学习模型中，神经网络被视为一系列非线性映射的组合，将输入数据从一个高维空间转换到另一个空间。这些映射可以用微分几何中的流形理论来解释，从而更深入地理解深度学习的工作原理。

神经网络层作为流形之间的映射

设输入数据分布在一个高维流形 $\mathcal{M}$ 上，神经网络的每一层都可以被视为一个从流形到流形的可微映射：

$$ f_i: \mathcal{M}{i-1} \rightarrow \mathcal{M}{i} $$

其中，$\mathcal{M}_0 = \mathcal{M}$，$\mathcal{M}_n$ 是第 $n$ 层的输出流形。通过复合映射，神经网络实现了从输入流形到输出流形的转换：

$$ F = f_n \circ f_{n-1} \circ \dots \circ f_1: \mathcal{M} \rightarrow \mathcal{N} $$

流形上的函数与特征提取

在微分几何中，流形上的函数可以描述局部和全局的几何特性。神经网络的激活函数和权重矩阵可以被视为定义在流形上的光滑函数：

• 激活函数：引入非线性，使得模型能够逼近任意复杂的函数，提供了流形之间非线性的可微映射。

• 权重矩阵：决定了映射的方向和尺度，对应于流形上的切向量场。

通过调整权重和偏置，神经网络在训练过程中学习到数据流形的几何结构，实现对数据特征的提取和表示。

优化过程中的几何视角

深度学习的训练过程是一个优化问题，目标是在参数空间中找到使损失函数最小化的参数组合。这个过程可以用黎曼几何中的概念来描述：

• 参数空间：所有可能的网络参数组合构成的空间，可以视为一个高维流形。

• 损失函数曲面：在参数空间上定义的标量场，每个点的值表示在该参数下模型的损失。

• 梯度下降法：在参数流形上沿着损失函数的最速下降方向移动，相当于在黎曼流形上寻找最短路径（测地线），以快速逼近损失函数的局部最小值。

深度学习中的曲率与泛化能力

微分几何中的曲率概念可以帮助理解深度学习模型的泛化能力：

• 平坦的最小值区域：在参数空间中，如果损失函数的最小值区域曲率较小（即更平坦），模型对参数扰动的不敏感性更高，泛化能力更强。

• 尖锐的最小值区域：曲率较大的区域，对参数变化非常敏感，可能导致过拟合，泛化能力较差。

通过将深度学习中的神经网络架构、训练过程和优化方法与微分几何中的流形、映射、曲率和测地线等概念对应起来，我们可以从几何的角度更深入地理解深度学习模型的内部机制。这种视角有助于揭示模型的本质特性，为改进深度学习算法提供新的思路。

3.4 深度学习与流形学习

3.4.1 流形学习

流形学习（Manifold Learning） 是一种非线性降维方法，旨在从高维数据中揭示低维的内在流形结构。流形学习假设高维数据实际上分布在一个低维的非线性流形 $\mathcal{M}$ 上，目标是找到一个映射函数 $\phi: \mathbb{R}^D \rightarrow \mathbb{R}^d$，其中 $d \ll D$，使得高维数据在低维空间中得到有效表示，同时保持原始数据的几何或拓扑特性。

常见的流形学习方法包括：

• 等距特征映射（Isomap）：基于测地距离的保持，通过最短路径计算近似测地距离。
• 局部线性嵌入（LLE）：保持数据局部邻域的线性重构关系。
• 拉普拉斯特征映射（Laplacian Eigenmaps）：利用图拉普拉斯算子捕捉数据的局部结构。

3.4.2 深度学习

深度学习（Deep Learning） 是一类基于多层神经网络的机器学习方法，通过组合多层非线性变换来学习数据的多级表示。深度学习模型试图逼近复杂的非线性函数，以从高维数据中抽取有用的特征，实现从输入到输出的映射。

数学上，深度神经网络的输出可以表示为嵌套的非线性函数：

$$ \mathbf{y} = f(\mathbf{x}; \theta) = f_L \circ f_{L-1} \circ \dots \circ f_1(\mathbf{x}) $$

其中，$\mathbf{x} \in \mathbb{R}^D$ 是输入数据，$\mathbf{y} \in \mathbb{R}^K$ 是输出，$f_l$ 表示第 $l$ 层的非线性映射，$\theta$ 是模型的参数集合。

3.4.3 流形学习与深度学习的关系

流形假设（Manifold Hypothesis） 是两者的共同基础，认为高维数据实际上集中在一个低维的流形结构上。深度学习和流形学习都试图捕捉这种低维结构，以实现数据的有效表示和处理。

• 特征表示：深度学习的隐藏层可以被视为将数据从原始空间映射到新的特征空间，逐层逼近数据的流形结构。
• 非线性映射：两者都利用非线性函数实现从高维空间到低维空间的映射。

3.4.4 流形学习与深度学习的区别

1. 模型结构和训练方式

   • 流形学习：通常是无参数或非参数模型，主要采用无监督学习方式，通过优化某种代价函数直接寻找低维嵌入。例如，LLE 通过最小化重构误差，找到保持局部结构的低维表示。
   • 深度学习：基于参数化的深层网络结构，包含大量的可训练参数，通过反向传播算法在监督或半监督的情况下进行训练，最小化任务相关的损失函数。

2. 泛化能力和可扩展性

   • 流形学习：由于方法的非参数性和计算复杂度限制，对新样本的映射和大规模数据处理存在困难。
   • 深度学习：具有良好的泛化能力，能够高效处理大规模数据，并对新样本进行快速预测。

3. 目标函数和优化

   • 流形学习：目标函数通常与数据的几何性质相关，如保持邻域关系或测地距离，优化过程涉及特征分解或凸优化。
   • 深度学习：目标函数与特定任务相关，如分类误差或重建误差，优化过程采用梯度下降等一阶方法，可能受到非凸性影响。

4. 理论基础

   • 流形学习：基于流形理论和非线性动力系统，强调数据的几何和拓扑结构。
   • 深度学习：涉及函数逼近理论、信息论和统计学习理论，关注模型的表达能力和泛化性能。

3.4.5 数学定理与理论差异

• 流形学习中的定理

  • Nash 嵌入定理：任何黎曼流形都可以等距地嵌入到欧氏空间中，保证了流形在高维空间中的表示。
  • 拉普拉斯-Beltrami 算子性质：用于捕捉流形的内在几何结构，常用于构建流形学习的目标函数。

• 深度学习中的定理

  • 通用逼近定理：单隐藏层神经网络在给定足够的神经元时，可以逼近任何连续函数。
  • 深度网络的表达能力定理：深度网络能够以指数级更少的参数表示某些函数，较浅层网络更具优势。

3.4.6 实际应用中的区别

• 流形学习：多用于数据可视化、降维和探索性数据分析，帮助理解数据的内在结构。
• 深度学习：广泛应用于图像识别、自然语言处理、语音识别等领域，解决实际的预测和分类问题。

深度学习和流形学习在目标上都有揭示高维数据的低维结构，但方法和应用领域有所不同。流形学习侧重于利用数据的几何性质进行降维，强调保持流形的结构，而深度学习通过训练深层网络从数据中学习特征表示，注重模型的预测性能。两者在理论基础和实际应用上都有所区别，但在理解和处理高维数据方面具有互补的作用。

3.5 数据的内蕴结构

根据流形假设，数据具有以下内蕴结构：

1. 低维度性：数据的有效维度远小于观测空间的维度。
2. 局部线性性：在流形的小邻域内，数据呈现线性特性。
3. 全局非线性性：整体上，数据分布体现出复杂的非线性结构，需要非线性方法来建模。

深度学习通过多层非线性变换，逐步提取数据的高级特征，能够有效捕捉数据的内在结构。其中，**自动编码器（Autoencoder）**利用编码器将数据映射到低维潜在空间，再通过解码器重建原始数据，学习到的数据表示即为内在结构。其模型表示为：

$$ \begin{align*} \text{编码器：} & \quad \mathbf{z} = f_{\text{enc}}(\mathbf{x}) \ \text{解码器：} & \quad \hat{\mathbf{x}} = f_{\text{dec}}(\mathbf{z}) \end{align*} $$

**卷积神经网络（CNN）则在图像等数据中，通过局部感受野和权值共享，提取空间局部特征，捕捉数据的内在结构。而生成对抗网络（GAN）**通过生成器和判别器的博弈，学习数据的分布，生成与真实数据相似的样本，进一步捕获数据的内在结构。

相对于深度学习，流形学习专注于揭示数据的低维流形结构，常用的方法有：等距映射（Isomap），利用测地距离替代欧氏距离，保持数据的全局几何结构；局部线性嵌入（LLE），保持数据的局部邻域几何结构，假设数据在局部邻域内可以用线性方式重构；以及拉普拉斯特征映射（LE），利用拉普拉斯矩阵，保持数据的局部邻域关系。

在应用与实践中，首先是降维与可视化，即将高维数据映射到低维空间，便于数据分析和可视化展示。其次是特征提取，获取数据的低维表示，提升机器学习模型的性能。最后是数据生成与复现，通过学习数据的内在结构，生成新的数据样本，用于数据增强等。

实例分析中，在人脸识别领域，人脸图像高维且受光照、表情等影响，但其变化受少数因素控制。使用深度学习模型（如深度卷积神经网络）提取的人脸特征，可以有效表示其内在结构，提高识别准确率。在自然语言处理方面，词嵌入模型（如 Word2Vec）将高维稀疏的词语表示为低维稠密向量，捕捉词语之间的语义关系，体现了数据的内在结构。

在方法的运用上，模型选择需要根据数据特性和任务需求，选择合适的深度学习或流形学习模型。参数调节则涉及调整模型的超参数（如学习率、网络层数）以更好地捕获数据结构。最后，模型融合通过结合深度学习和流形学习的方法，提升模型的表达能力和泛化性能。

通过深度学习和流形学习的方法，可以洞察数据的一些内在结构和特征，但不是全部。单纯依靠几何和统计的方法不足以全面捕捉数据的复杂性。为了更深入地理解数据的整体形态和潜在模式，需要引入拓扑学的视角。拓扑数据分析（Topological Data Analysis，TDA）作为一种新兴的方法，是从全局的角度揭示数据的形状特征，帮助发现传统方法难以识别的数据深层次结构。

4. 拓扑数据分析(TDA)

拓扑数据分析(Topological Data Analysis, TDA)是一种结合拓扑学和数据科学的现代分析方法，它通过研究数据的形状和结构特征来获取洞察。TDA的核心思想是数据具有“形状“，这种形状包含了重要的信息，可以通过持续同调(Persistent Homology)等工具来捕获。

TDA的主要技术包括：将点云数据转化为简单复形(Simplicial Complex)序列，计算持续图(Persistence Diagram)和条形码(Barcode)来表示拓扑特征的“寿命“，以及使用Mapper算法构建数据的拓扑骨架。这种方法特别适合分析高维、非线性和噪声数据，因为它对数据变形具有鲁棒性，能够捕获数据的本质拓扑特征。在实践中，TDA已被成功应用于基因组学、材料科学、金融市场分析等领域，帮助发现传统方法难以识别的数据模式和结构。TDA不仅提供了一种新的数据分析视角，也为数据价值评估提供了基于拓扑特征的量化指标。

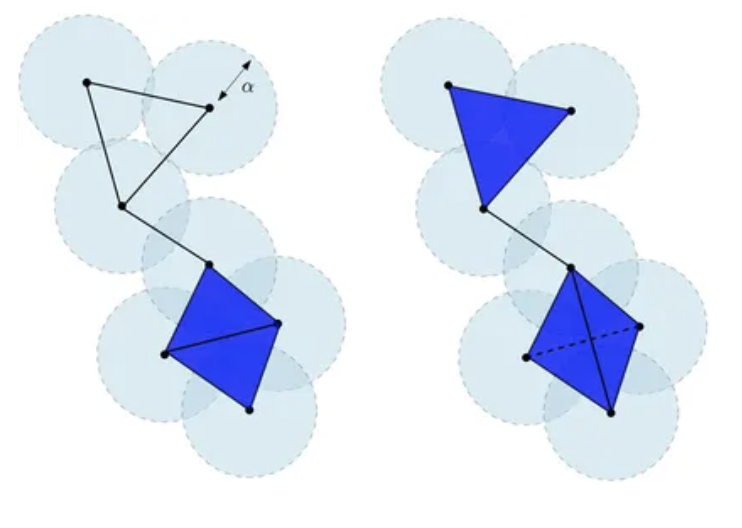
图例中所示平面 $\mathbb{R}^2$ 中有限点云的切赫复形 $\text{Cech}\alpha(X)$（左）和维托里斯-里普斯复形 $\text{Rips}{2\alpha}(X)$（右）。$\text{Cech}\alpha(X)$ 的底部是两个相邻三角形的并集，而 $\text{Rips}{2\alpha}(X)$ 的底部是由四个顶点及其所有面构成的四面体。切赫复形的维数是2。维托里斯-里普斯复形的维数是3。

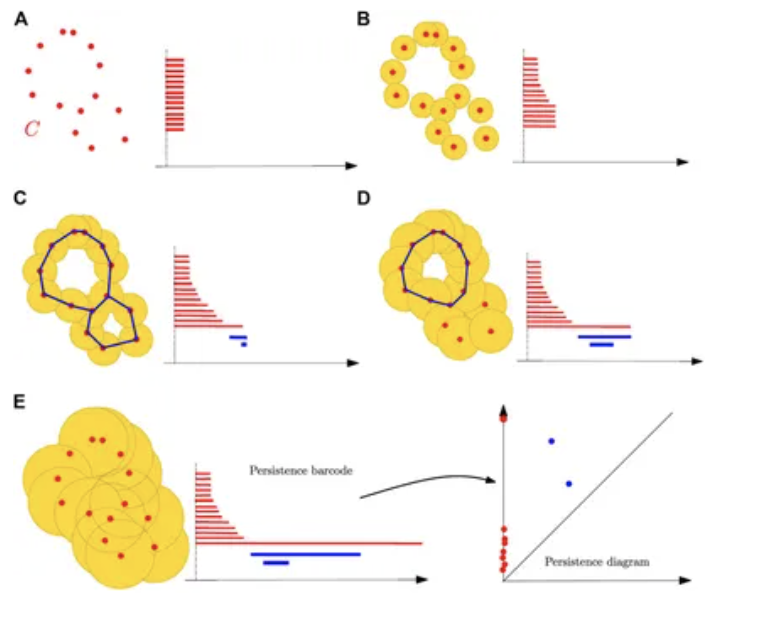
点云距离函数的子水平集过滤以及随着球体半径增加构造其持续条形码的过程。球体并集中的蓝色曲线表示与条形码中蓝色条相关的一维循环。持续图最终由持续条形码定义。

(A) 当半径 r = 0 时,球体的并集简化为初始有限点集,每个点对应一个零维特征,即连通分量;在 r = 0 时为每个特征的诞生创建一个区间。

(B) 一些球体开始重叠,导致一些连通分量合并而消失;持续图通过在相应区间消失时添加终点来记录这些死亡。

(C) 新的分量已合并,形成单个连通分量,因此除了剩余分量对应的区间外,所有与零维特征相关的区间都已结束;出现了两个新的一维特征,在其诞生尺度上产生两个新的区间(蓝色)。

(D) 两个一维循环中的一个已被填充,导致其在过滤中消失以及相应蓝色区间的结束。

(E) 所有一维特征都已消失;只剩下长的(且永不消失的)红色区间。与前面的例子一样,最终的条形码也可以等价地表示为持续图,其中每个区间(a,b)由 $\mathbb{R}^2$ 中坐标为(a,b)的点表示。直观地说,条形码中的区间越长,或等价地,图中相应点离对角线越远,相应的同调特征在过滤中就越持久,因此越重要。还要注意,对于给定半径 r,相应球体并集的第 k 个贝蒂数等于包含 r 的 k 维同调特征对应的持续区间数。因此,持续图可以被视为一个多尺度拓扑特征,它编码了球体并集在所有半径下的同调以及其随 r 值变化的演化。

4.1 TDA的主要数学定理

1. 持续同调基本定理：

   • 任何持续模都可以被唯一分解为区间模的直和
   • 持续图完全表征了持续同调群的代数结构
   • 形式化表示：$H_n(X) \cong \bigoplus_{i=1}^k I[b_i,d_i)$

2. 稳定性定理：

   • 对于两个紧致度量空间的持续图，其瓶颈距离有上界
   • $d_B(Dgm(f),Dgm(g)) \leq ||f-g||_{\infty}$
   • 保证了TDA方法对噪声的鲁棒性

3. Nerve定理：

   • 将覆盖的神经复形与原空间的同伦等价性联系起来
   • 对于一个好的覆盖$\mathcal{U}$，其神经复形$N(\mathcal{U})$与原空间$X$同伦等价

4. Mapper算法收敛定理：

   • 在合适条件下，Mapper输出会收敛到原始空间的Reeb图
   • 为Mapper算法提供了理论保证

4.2 TDA的实际应用案例

1. 生物医学领域：

   • 乳腺癌亚型识别：通过分析基因表达数据的拓扑特征
   • 蛋白质构象分析：研究蛋白质折叠过程中的构象变化
   • 示例：使用持续同调分析基因表达数据

2. 材料科学：

   • 材料微观结构分析：研究材料的孔隙分布和连通性
   • 相变过程研究：捕捉材料在相变过程中的结构变化
   • 应用：分析多孔材料的结构特征

3. 金融市场分析：

   • 市场结构研究：分析金融资产之间的关联性
   • 风险评估：识别市场的系统性风险模式
   • 实例：股票市场网络分析

4. 图像处理与计算机视觉：

   • 形状识别：基于拓扑特征的物体识别
   • 图像分割：利用持续同调进行图像分割
   • 应用：目标检测中的形状描述

5. 社交网络分析：

   • 社区结构识别：发现网络中的社区和层次结构
   • 信息传播模式：分析信息在网络中的扩散特征
   • 示例：社区检测

5. 数据流形与数据拓扑的异同

数据流形与数据拓扑是数据分析领域中刻画高维数据结构的重要概念。二者都涉及对数据的内在几何和拓扑结构的理解，但在理论基础和应用上存在一定的区别。

5.1 数据流形

数据流形理论假设高维数据实际上位于比原始空间低维的嵌入式流形上。即给定的高维数据集 $X \subset \mathbb{R}^D$，假定存在一个 $d$ 维流形 $\mathcal{M}$（其中 $d < D$），使得数据点集中在 $\mathcal{M}$ 上或其附近。数据流形理论的主要目标是通过降维或嵌入技术，如 Isomap、LLE、t-SNE 等，将高维数据映射到低维空间，同时保留数据的几何结构。

5.2 数据拓扑

数据拓扑，特别是基于拓扑数据分析（TDA）的方法，更关注数据的全局拓扑特征，如连通性、孔洞和空腔等。通过构建如持续同调、持续条形码等工具，TDA 能够在不同尺度下捕捉数据的拓扑特征，从而揭示数据的形状和结构，而不局限于特定的维度或几何形状。

5.3 二者的相同点

1. 关注数据的内在结构：数据流形和数据拓扑都试图理解数据的内在结构，超越单纯的坐标表示，挖掘数据点之间的本质关联。

2. 抗噪性和鲁棒性：二者都具备一定的抗噪性，能够在一定程度上忽略数据中的噪声和异常值，专注于数据的核心结构。

3. 高维数据分析：两种方法都适用于高维数据的分析，帮助研究者克服维度灾难的问题。

5.4 二者的不同点

1. 理论基础不同：数据流形基于流形理论和微分几何，侧重于局部几何结构的保留；而数据拓扑基于代数拓扑和同调理论，关注全局拓扑性质。

2. 关注尺度不同：数据流形方法通常专注于数据的局部结构，保持近邻关系；而数据拓扑方法则在不同尺度下分析数据，捕捉全局拓扑特征。

3. 应用目标不同：数据流形主要用于降维、可视化和特征提取，强调数据的嵌入表示；数据拓扑则用于形状分析、模式识别和结构发现，强调数据的拓扑不变量。

4. 算法工具不同：数据流形采用如 PCA、MDS、LLE、Isomap 等降维算法；数据拓扑采用持续同调、Čech 复形、Rips 复形等拓扑计算工具。

在实际应用中，数据流形和数据拓扑的方法可以结合使用，以获得对数据结构更全面的理解。例如，先利用流形学习方法进行降维，再应用拓扑数据分析提取拓扑特征，或反之。这样可以同时利用几何和拓扑的信息，提高数据分析的效果。

数据流形和数据拓扑的概念是理解数据价值的基础。数据的内蕴结构直接影响其潜在价值，理解这些结构有助于我们准确地挖掘和量化数据的价值。接下来，我们将探讨数据价值的起源，揭示数据为何具有价值。

第二章 数据价值的起源

数据的价值源于其所包含的信息。数据本身只是一些符号和数字的集合，但通过分析和处理这些数据，我们可以从中提取出有用的信息。这些信息可以帮助我们理解复杂的现象、做出明智的决策、预测未来的趋势以及发现新的知识和洞见。

信息的获取过程通常涉及对数据的收集、清洗、分析和解释。高质量的数据能够提供准确、及时和相关的信息，从而在决策过程中发挥重要作用。例如，在商业领域，企业可以通过分析销售数据来了解市场需求，优化库存管理，制定营销策略，从而提高盈利能力。在科学研究中，数据分析可以揭示自然现象的规律，推动技术创新和科学进步。

然而，数据的价值不仅取决于其自身，还取决于我们对其进行处理和分析的能力。先进的数据分析技术和工具，如机器学习、人工智能和大数据分析，能够从海量数据中挖掘出有价值的信息，提升数据的利用价值。因此，数据的价值不仅在于其所包含的信息量，还在于我们能够从中提取和利用这些信息的能力。

2.1 从瞎子摸象到冷冻电镜技术

瞎子摸象的两种场景

场景一：瞎子之间各自不交换信息

在这个场景中，几个瞎子被带到一头大象面前，他们被要求描述大象的样子。由于他们无法看到，只能通过触摸来感知大象的形状。每个瞎子触摸大象的不同部位，例如象鼻、象腿、象耳等。由于他们没有交换信息，每个人只能根据自己触摸到的部分来描述大象。

• 一个触摸到象鼻的瞎子可能会说：“大象像一条粗大的蛇。”
• 另一个触摸到象腿的瞎子可能会说：“不对，大象像一根粗壮的柱子。”
• 触摸到象耳的瞎子则会说：“你们都错了，大象像一把大扇子。”

由于每个瞎子只触摸到大象的一部分，他们的描述各不相同，甚至相互矛盾。最终，他们无法达成一致的结论，每个人都坚持自己的观点。这种情况下，信息的孤立和缺乏交流导致了对整体的误解。

场景二：瞎子之间充分交换信息

在这个场景中，几个瞎子同样被带到一头大象面前，他们被要求描述大象的样子。但这次，他们在触摸大象的不同部位后，开始相互交流和分享各自的感受和发现。

• 触摸到象鼻的瞎子说：“我感觉大象的鼻子像一条粗大的蛇。”
• 触摸到象腿的瞎子回应：“我触摸到的象腿像一根粗壮的柱子。”
• 触摸到象耳的瞎子补充道：“而我触摸到的象耳像一把大扇子。” …

通过充分的交流和信息共享，他们逐渐意识到每个人触摸到的只是大象的一部分。通过整合各自的信息，他们可以拼凑出大象的整体形象。数学上可以证明，通过足够的信息交换和整合，瞎子们可以联合起来识别出大象的全貌。

冷冻电镜技术：瞎子摸象的实现

冷冻电镜技术本质上就是瞎子摸象的第二种场景的实现。通过对样本的不同部分进行成像，并将这些信息整合起来，科学家们能够重建出样本的三维结构，从而获得对其整体形态的准确理解。

冷冻电镜技术的原理

冷冻电镜（Cryo-Electron Microscopy, Cryo-EM）是一种用于观察生物大分子和细胞结构的高分辨率成像技术。其基本原理包括以下几个步骤：

1. 样本制备：

   • 样本被快速冷冻到液氮温度（约-196°C），以保持其天然状态并防止辐射损伤。快速冷冻的过程可以形成无定形冰，而不是晶体冰，从而避免了冰晶对样本结构的破坏。

2. 数据采集：

   • 冷冻样本被放置在透射电子显微镜（Transmission Electron Microscope, TEM）中进行成像。电子束穿过样本，形成二维投影图像。为了获得样本的三维结构，需要从不同角度采集大量的二维图像。

3. 图像处理：

   • 采集到的二维图像经过对齐、分类和平均处理，以提高信噪比和分辨率。通过对大量图像进行统计分析，可以消除噪声和变形，提取出样本的真实结构信息。

4. 三维重建：

   • 利用计算机算法将处理后的二维图像进行三维重建。常用的方法包括单颗粒重构（Single Particle Reconstruction）和电子断层扫描（Electron Tomography）。单颗粒重构适用于对称性较高的样本，而电子断层扫描则适用于复杂的细胞和组织样本。

5. 结构解析：

   • 重建出的三维结构可以用于进一步的结构解析和功能研究。科学家们可以通过分析三维结构，了解生物大分子的构象变化、相互作用和功能机制。

冷冻电镜技术的优势在于其能够在接近生理条件下观察生物样本，避免了传统方法中样本制备过程对结构的破坏。此外，冷冻电镜技术不需要晶体化样本，适用于研究难以结晶的生物大分子，如膜蛋白和大分子复合物。

近年来，随着冷冻电镜技术的发展和电子显微镜分辨率的提高，科学家们已经能够解析出原子级分辨率的生物大分子结构。这为生命科学研究提供了强有力的工具，推动了结构生物学、药物设计和分子生物学等领域的进步。

数学证明：从二维投影重构三维结构

冷冻电镜技术能够通过大量的二维投影图像重构出样本的三维结构，这一过程可以通过数学上的逆投影原理（Inverse Projection Principle）来解释。以下是这一原理的简要证明：

1. 投影定理：

   • 在傅里叶变换的框架下，投影定理（Projection-Slice Theorem）指出，一个三维物体的二维投影的傅里叶变换等于该物体的三维傅里叶变换在相应平面上的切片。具体来说，设 $f(x, y, z)$ 是三维物体的密度函数，其在平面 $z = 0$ 上的投影为： $$ P(x, y) = \int_{-\infty}^{\infty} f(x, y, z) , dz $$ 则 $P(x, y)$ 的傅里叶变换 $F_P(u, v)$ 等于 $f(x, y, z)$ 的傅里叶变换 $F(u, v, w)$ 在 $w = 0$ 平面上的切片： $$ F_P(u, v) = F(u, v, 0) $$

2. 逆投影原理：

   • 根据投影定理，我们可以通过采集不同角度的二维投影图像，获得三维物体在不同平面上的傅里叶切片。设 $P_\theta(x’, y’)$ 是物体在角度 $\theta$ 下的投影，其傅里叶变换为 $F_{P_\theta}(u’, v’)$。通过对所有角度的投影进行傅里叶变换，我们可以得到三维傅里叶空间中的一系列切片。

3. 重建三维结构：

   • 通过将这些切片组合起来，我们可以重建出三维物体的傅里叶变换 $F(u, v, w)$。然后，通过对 $F(u, v, w)$ 进行逆傅里叶变换，我们可以得到原始的三维密度函数 $f(x, y, z)$： $$ f(x, y, z) = \mathcal{F}^{-1}{F(u, v, w)} $$
   • 其中，$\mathcal{F}^{-1}$ 表示逆傅里叶变换。

4. 实际应用：

   • 在冷冻电镜技术中，样本的二维投影图像是从不同角度采集的。通过对这些图像进行傅里叶变换，并利用逆投影原理，我们可以重建出样本的三维结构。这一过程通常需要大量的计算和图像处理技术，以确保重建结果的准确性和分辨率。

数学证明：冷冻电镜技术与瞎子模型的本质相同

在冷冻电镜技术中，我们通过从不同角度采集样本的二维投影图像，利用数学上的逆投影原理重构出样本的三维结构。这一过程可以通过数学的群论来解释，证明其与瞎子摸象的第二个场景的本质是一样的。

1. 群的定义：

   • 在数学中，群（Group）是一个由元素组成的集合，并且在集合上定义了一种二元运算，使得该集合在此运算下满足封闭性、结合性、单位元存在性和逆元存在性。设 $G$ 是一个群，$e$ 是单位元，$a, b \in G$，则有：
     1. 封闭性：对于任意 $a, b \in G$，有 $a \cdot b \in G$。
     2. 结合性：对于任意 $a, b, c \in G$，有 $(a \cdot b) \cdot c = a \cdot (b \cdot c)$。
     3. 单位元存在性：存在单位元 $e \in G$，使得对于任意 $a \in G$，有 $a \cdot e = e \cdot a = a$。
     4. 逆元存在性：对于任意 $a \in G$，存在逆元 $a^{-1} \in G$，使得 $a \cdot a^{-1} = a^{-1} \cdot a = e$。

2. 冷冻电镜技术中的群作用：

   • 在冷冻电镜技术中，我们可以将样本的不同角度的二维投影图像视为群 $G$ 的元素。设 $f(x, y, z)$ 是三维物体的密度函数，其在不同角度 $\theta$ 下的投影为 $P_\theta(x’, y’)$。这些投影图像可以通过群作用 $g \in G$ 进行变换，表示为 $g \cdot P(x, y)$，其中 $g$ 是一个旋转操作。

3. 瞎子摸象的群作用：

   • 在瞎子摸象的第二个场景中，每个盲人通过触摸大象的不同部位来描述大象的形状。我们可以将每个盲人的触摸视为群 $G$ 的元素。设 $E$ 是大象的整体形状，其在不同盲人触摸下的局部信息为 $E_i$。这些局部信息可以通过群作用 $g \in G$ 进行变换，表示为 $g \cdot E$，其中 $g$ 是一个局部触摸操作。

4. 群作用的等价性：

   • 在冷冻电镜技术和瞎子摸象的场景中，群作用的本质是一样的。通过不同角度的投影图像或局部触摸信息，我们可以获得样本或大象的局部信息。利用群作用的封闭性和结合性，我们可以将这些局部信息整合起来，重构出样本的三维结构或大象的整体形状。

5. 重建过程的数学证明：

   • 设 $G$ 是一个群，$f(x, y, z)$ 是三维物体的密度函数，其在不同角度 $\theta$ 下的投影为 $P_\theta(x’, y’)$。通过群作用 $g \in G$，我们可以获得一系列投影图像 $g \cdot P(x, y)$。利用逆投影原理，我们可以将这些投影图像的傅里叶变换 $F_{P_\theta}(u’, v’)$ 组合起来，重建出三维物体的傅里叶变换 $F(u, v, w)$，进而通过逆傅里叶变换得到原始的三维密度函数 $f(x, y, z)$。

2.2 信息的数学表达

冷冻电镜技术通过从不同角度采集大量的二维投影图像，利用数学上的逆投影原理重构出样本的三维结构。这一过程类似于将瞎子摸象的各个局部信息整合起来，形成对大象的完整认知。

在大数据分析中，我们面临着比冷冻电镜技术更高维度的数据。尽管数据维度增加，但背后的数学原理依然适用。从数据流形和数据拓扑的视角来看，冷冻电镜技术与大数据分析存在深刻的数学联系。

从流形的角度，冷冻电镜技术本质上是在重建样本所在的三维流形结构。每张二维投影图像可以视为这个三维流形在特定方向上的切片。类似地，高维数据分析中，数据点分布在某个低维流形上，我们通过不同维度的观测获得这个流形的局部切片。设高维数据集 $D$ 位于流形 $\mathcal{M}$ 上，每个观测视角 $\theta$ 对应一个局部坐标图 $\phi_\theta: U_\theta \rightarrow \mathbb{R}^k$，其中 $U_\theta$ 是流形上的开集。这些局部坐标图的拼接重建了整个流形结构。

从拓扑的角度，冷冻电镜技术通过分析不同投影角度下的持续同调特征来重建样本的拓扑结构。每个投影角度捕捉了样本在该方向上的拓扑特征，如连通分支、空洞等。在高维数据分析中，我们同样可以研究数据在不同尺度和视角下的拓扑特征。设 $f_\theta: D \rightarrow \mathbb{R}^k$ 是数据在视角 $\theta$ 下的过滤函数，通过计算持续同调群：

$$H_n(f_\theta^{-1}(-\infty, t]) \rightarrow H_n(f_\theta^{-1}(-\infty, s])$$

其中 $t < s$ 是过滤参数，$H_n$ 表示 $n$ 维同调群。这些持续同调特征的综合反映了数据的全局拓扑结构。

数据是信息在局部空间的投影

从流形的角度，冷冻电镜技术本质上是在重建样本所在的三维流形结构。每张二维投影图像可以视为这个三维流形在特定方向上的切片。类似地，高维数据分析中，数据点分布在某个低维流形上，我们通过不同维度的观测获得这个流形的局部切片。设高维数据集 $D$ 位于流形 $\mathcal{M}$ 上，每个观测视角 $\theta$ 对应一个局部坐标图 $\phi_\theta: U_\theta \rightarrow \mathbb{R}^k$，其中 $U_\theta$ 是流形上的开集。这些局部坐标图的拼接重建了整个流形结构。

从拓扑的角度，冷冻电镜技术通过分析不同投影角度下的持续同调特征来重建样本的拓扑结构。每个投影角度捕捉了样本在该方向上的拓扑特征，如连通分支、空洞等。在高维数据分析中，我们同样可以研究数据在不同尺度和视角下的拓扑特征。设 $f_\theta: D \rightarrow \mathbb{R}^k$ 是数据在视角 $\theta$ 下的过滤函数，通过计算持续同调群：

$$H_n(f_\theta^{-1}(-\infty, t]) \rightarrow H_n(f_\theta^{-1}(-\infty, s])$$

其中 $t < s$ 是过滤参数，$H_n$ 表示 $n$ 维同调群。这些持续同调特征的综合反映了数据的全局拓扑结构。

综上所述，数据是信息在某个局部空间的投影。无论是瞎子摸象、冷冻电镜技术，还是大数据分析，都是通过对数据的整合和分析，来重建全局信息的过程。理解这一点，对于我们全面、准确地分析和利用数据具有重要意义。

信息熵

信息熵（Entropy）是信息论中的一个核心概念，由克劳德·香农（Claude Shannon）在其1948年的论文《通信的数学理论》中提出。信息熵用于度量信息的不确定性或随机性。具体来说，信息熵衡量的是在一个随机变量的所有可能取值中，平均每个取值所包含的信息量。

设有一个离散随机变量 $X$，其可能取值为 ${x_1, x_2, \ldots, x_n}$，对应的概率分布为 ${p_1, p_2, \ldots, p_n}$，其中 $p_i = P(X = x_i)$。信息熵 $H(X)$ 定义为：

$$ H(X) = -\sum_{i=1}^n p_i \log p_i $$

在上述公式中，$\log$ 通常取以2为底，这样信息熵的单位是比特（bit）。如果取自然对数，则单位是纳特（nat）。

信息熵的值越大，表示随机变量的不确定性越高，包含的信息量也越大。反之，信息熵的值越小，表示随机变量的不确定性越低，包含的信息量也越小。

香农定理

香农定理（Shannon’s Theorem），也称为香农信息论的基本定理，主要包括两个部分：香农第一定理（无噪信道编码定理）和香农第二定理（有噪信道编码定理）。

1. 香农第一定理（无噪信道编码定理）：

   香农第一定理指出，对于一个无噪信道，存在一种编码方法，使得信息可以以接近信道容量的速率进行无误传输。信道容量 $C$ 是信道能够无误传输信息的最大速率，定义为：

   $$ C = \max_{p(x)} I(X; Y) $$

   其中，$I(X; Y)$ 是输入 $X$ 和输出 $Y$ 之间的互信息，$p(x)$ 是输入的概率分布。

2. 香农第二定理（有噪信道编码定理）：

   香农第二定理指出，对于一个有噪信道，如果信息传输速率低于信道容量 $C$，则存在一种编码方法，使得误码率可以任意小。反之，如果信息传输速率超过信道容量，则无论采用何种编码方法，误码率都无法避免。

费舍尔信息

费舍尔信息（Fisher Information）是统计学中的一个重要概念，用于度量参数估计中的信息量。它由统计学家罗纳德·费舍尔（Ronald Fisher）提出，主要用于评估估计量的精确度。费舍尔信息在参数估计、实验设计和机器学习等领域具有广泛应用。

设有一个参数为 $\theta$ 的概率密度函数 $f(x; \theta)$，其中 $x$ 是观测数据。费舍尔信息 $I(\theta)$ 定义为对数似然函数的二阶导数的期望值，即：

$$ I(\theta) = \mathbb{E} \left[ \left( \frac{\partial}{\partial \theta} \log f(X; \theta) \right)^2 \right] $$

其中，$\mathbb{E}$ 表示期望值，$\log f(X; \theta)$ 是对数似然函数。

费舍尔信息的值越大，表示参数估计的精确度越高。费舍尔信息矩阵是费舍尔信息的多维推广，用于多参数估计问题。

克拉美-罗下界

克拉美-罗下界（Cramér-Rao Lower Bound, CRLB）是统计学中的一个重要定理，用于给出参数估计的方差的下界。它表明，对于任意无偏估计量，其方差不能小于费舍尔信息的倒数。具体来说，设 $\hat{\theta}$ 是参数 $\theta$ 的无偏估计量，则有：

$$ \text{Var}(\hat{\theta}) \geq \frac{1}{I(\theta)} $$

其中，$\text{Var}(\hat{\theta})$ 表示估计量 $\hat{\theta}$ 的方差，$I(\theta)$ 是费舍尔信息。

克拉美-罗下界为评估估计量的性能提供了一个理论基准，任何无偏估计量的方差都不能低于这个下界。

互信息

互信息（Mutual Information）是信息论中的一个重要概念，用于度量两个随机变量之间的相互依赖性。互信息反映了一个随机变量包含的关于另一个随机变量的信息量。设有两个随机变量 $X$ 和 $Y$，其联合概率分布为 $p(x, y)$，边缘概率分布分别为 $p(x)$ 和 $p(y)$。互信息 $I(X; Y)$ 定义为：

$$ I(X; Y) = \sum_{x \in X} \sum_{y \in Y} p(x, y) \log \frac{p(x, y)}{p(x) p(y)} $$

互信息的值越大，表示两个随机变量之间的依赖性越强。互信息在特征选择、聚类分析和图像处理等领域具有广泛应用。

卡尔曼滤波

卡尔曼滤波（Kalman Filtering）是一种递归算法，用于估计动态系统的状态。它由鲁道夫·卡尔曼（Rudolf Kalman）提出，广泛应用于信号处理、控制系统和导航等领域。卡尔曼滤波通过结合系统的先验信息和观测数据，递归地更新状态估计。

卡尔曼滤波的基本步骤包括预测和更新两个阶段：

1. 预测阶段：根据系统的状态转移模型，预测下一个时刻的状态和协方差矩阵。
2. 更新阶段：根据观测数据，更新状态估计和协方差矩阵。

卡尔曼滤波的数学表达如下：

预测阶段： $$ \hat{x}{k|k-1} = A \hat{x}{k-1|k-1} + B u_k $$ $$ P_{k|k-1} = A P_{k-1|k-1} A^T + Q $$

更新阶段： $$ K_k = P_{k|k-1} H^T (H P_{k|k-1} H^T + R)^{-1} $$ $$ \hat{x}{k|k} = \hat{x}{k|k-1} + K_k (z_k - H \hat{x}{k|k-1}) $$ $$ P{k|k} = (I - K_k H) P_{k|k-1} $$

其中，$\hat{x}{k|k-1}$ 是预测状态，$P{k|k-1}$ 是预测协方差矩阵，$K_k$ 是卡尔曼增益矩阵，$z_k$ 是观测数据，$H$ 是观测矩阵，$Q$ 是过程噪声协方差矩阵，$R$ 是观测噪声协方差矩阵。

信息几何

信息几何（Information Geometry）是研究概率分布空间几何结构的数学理论。它结合了微分几何和信息论的概念，用于分析统计模型和机器学习算法的性质。信息几何的核心思想是将概率分布视为流形，并在其上定义几何结构，如度量、连接和曲率。

1. 概率分布流形：

   • 概率分布流形是由一组概率分布组成的流形。设 $\mathcal{P}$ 是一个概率分布族，每个分布 $p(x; \theta)$ 由参数 $\theta$ 确定，其中 $\theta$ 是一个 $d$ 维向量。概率分布流形 $\mathcal{M}$ 可以表示为 $\mathcal{M} = { p(x; \theta) \mid \theta \in \Theta }$，其中 $\Theta$ 是参数空间。

2. Fisher 信息度量：

   • Fisher 信息度量是定义在概率分布流形上的度量张量。对于参数 $\theta$，Fisher 信息度量 $g_{ij}(\theta)$ 定义为： $$ g_{ij}(\theta) = \mathbb{E} \left[ \frac{\partial \log p(x; \theta)}{\partial \theta^i} \frac{\partial \log p(x; \theta)}{\partial \theta^j} \right] $$ 其中，$\mathbb{E}$ 表示期望值，$i$ 和 $j$ 是参数的索引。Fisher 信息度量度量了参数空间中微小变化对概率分布的影响。

3. Kullback-Leibler 散度：

   • Kullback-Leibler (KL) 散度是度量两个概率分布之间差异的非对称度量。对于两个概率分布 $p(x)$ 和 $q(x)$，KL 散度定义为： $$ D_{KL}(p | q) = \sum_{x} p(x) \log \frac{p(x)}{q(x)} $$ 在信息几何中，KL 散度可以用来定义概率分布流形上的距离。

主要定理

1. Cramér-Rao 不等式：

   • Cramér-Rao 不等式是统计估计理论中的一个重要结果。它给出了无偏估计量方差的下界。设 $\hat{\theta}$ 是参数 $\theta$ 的无偏估计量，$I(\theta)$ 是 Fisher 信息矩阵，则有： $$ \text{Var}(\hat{\theta}) \geq \frac{1}{I(\theta)} $$ 其中，$\text{Var}(\hat{\theta})$ 表示估计量 $\hat{\theta}$ 的方差。Cramér-Rao 不等式表明，任何无偏估计量的方差都不能低于这个下界。

2. Jeffreys Prior：

   • Jeffreys Prior 是一种无信息先验分布，用于贝叶斯统计中。它基于 Fisher 信息度量定义，表示为： $$ \pi(\theta) \propto \sqrt{\det I(\theta)} $$ 其中，$\det I(\theta)$ 是 Fisher 信息矩阵的行列式。Jeffreys Prior 在参数空间中是平移不变的，适用于没有先验信息的情况。

3. Pythagorean 定理：

   • 在信息几何中，Pythagorean 定理描述了概率分布流形上的正交投影性质。设 $p(x; \theta)$ 是概率分布流形上的一个点，$q(x)$ 是流形外的一个点，$r(x)$ 是 $q(x)$ 在流形上的正交投影点，则有： $$ D_{KL}(q | p) = D_{KL}(q | r) + D_{KL}(r | p) $$ 该定理表明，KL 散度在正交投影过程中满足类似于欧几里得空间中的勾股定理。

信息几何为理解和分析复杂统计模型提供了强大的工具。通过将概率分布视为几何对象，我们可以更直观地研究其性质和关系，从而在机器学习和统计推断中获得更深刻的洞见。

2.3 数据价值与信息价值

数据价值与信息价值之间存在几个主要特点，这些特点在信息的数学表达中得到了体现：

1. 非线性：

   • 数据与信息之间的关系通常是非线性的。简单的数据变换可能会导致信息的显著变化，反之亦然。例如，非线性变换（如对数变换、指数变换）在数据处理中常用于揭示隐藏的模式和关系。信息几何中的Fisher信息度量和KL散度等工具可以帮助我们理解这种非线性关系。

2. 非完备：

   • 数据通常是不完备的，可能存在缺失值、噪声和不确定性。这种非完备性会影响信息的提取和利用。信息几何中的Cramér-Rao不等式提供了无偏估计量方差的下界，表明在不完备数据下，估计的精度受到限制。非完备数据需要通过数据清洗、插值和建模等方法进行处理，以提高信息的质量。

3. 不可逆：

   • 数据到信息的转换过程通常是不可逆的。一旦信息从数据中提取出来，原始数据可能无法完全恢复。例如，数据压缩和降维技术在保留主要信息的同时丢失了一些细节。信息几何中的Pythagorean定理描述了KL散度在正交投影过程中的性质，表明信息的丢失是不可避免的。

4. 信息的多尺度性：

   • 信息可以在不同的尺度上进行分析和提取。数据的多尺度特性使得我们可以从宏观和微观两个层面理解信息。例如，拓扑数据分析（TDA）通过在不同尺度下捕捉数据的拓扑特征，揭示数据的全局结构和局部模式。多尺度分析有助于全面理解数据的内在结构和信息价值。

5. 信息的上下文依赖性：

   • 信息的价值往往依赖于其上下文和应用场景。同样的数据在不同的背景下可能具有不同的意义和价值。例如，在商业领域，销售数据可以用于市场分析和需求预测；在医疗领域，患者数据可以用于疾病诊断和治疗方案制定。信息几何提供了分析不同上下文中信息变化的工具，帮助我们理解信息的上下文依赖性。

6. 信息的动态性：

   • 信息是动态变化的，随着时间和环境的变化而变化。数据的时序特性和动态变化需要通过时间序列分析和动态建模来捕捉。例如，卡尔曼滤波器用于动态系统的状态估计，能够在噪声和不确定性下提供实时信息更新。信息几何中的动态度量和连接可以帮助我们理解信息的动态变化。

数据价值与信息价值的泛函关系

我们可以通过数学的方法论证数据的价值与信息价值之间的泛函关系。假设数据集为 $D$，信息为 $I$，我们可以定义一个泛函 $F$ 来描述数据到信息的转换过程：

$$ I = F(D) $$

其中，$F$ 是一个非线性、非完备、不可逆的映射。为了进一步分析这种关系，我们可以引入一些数学工具和定理。

1. 非线性关系： 假设 $F$ 是一个非线性变换，可以表示为： $$ I = F(D) = g(D) $$ 其中，$g$ 是一个非线性函数。为了揭示这种非线性关系，我们可以使用泰勒展开式对 $g(D)$ 进行近似： $$ g(D) \approx g(D_0) + \nabla g(D_0) \cdot (D - D_0) + \frac{1}{2} (D - D_0)^T H_g(D_0) (D - D_0) $$ 其中，$D_0$ 是数据的某个参考点，$\nabla g(D_0)$ 是 $g$ 在 $D_0$ 处的梯度，$H_g(D_0)$ 是 $g$ 在 $D_0$ 处的 Hessian 矩阵。

2. 非完备性： 数据的不完备性可以通过引入噪声模型来描述。假设数据 $D$ 包含噪声 $\epsilon$，则有： $$ D = D_{\text{true}} + \epsilon $$ 其中，$D_{\text{true}}$ 是真实数据，$\epsilon$ 是噪声。根据 Cramér-Rao 不等式，估计量的方差有下界： $$ \text{Var}(\hat{\theta}) \geq \frac{1}{I(\theta)} $$ 这表明在不完备数据下，信息的提取精度受到限制。

3. 不可逆性： 数据到信息的转换过程通常是不可逆的。假设 $F$ 是一个不可逆映射，则存在信息丢失。根据 Pythagorean 定理，KL 散度在正交投影过程中满足： $$ D_{KL}(q | p) = D_{KL}(q | r) + D_{KL}(r | p) $$ 这表明信息的丢失是不可避免的。

4. 信息的多尺度性： 信息可以在不同的尺度上进行分析。假设 $F$ 包含多尺度分析，则有： $$ I = F(D) = \sum_{i=1}^n F_i(D) $$ 其中，$F_i$ 表示在第 $i$ 个尺度上的信息提取。拓扑数据分析（TDA）通过在不同尺度下捕捉数据的拓扑特征，揭示数据的全局结构和局部模式。

5. 信息的上下文依赖性： 信息的价值依赖于其上下文。假设 $F$ 包含上下文依赖性，则有： $$ I = F(D, C) $$ 其中，$C$ 表示上下文信息。信息几何提供了分析不同上下文中信息变化的工具。

6. 信息的动态性： 信息是动态变化的。假设 $F$ 包含动态变化，则有： $$ I(t) = F(D(t)) $$ 其中，$t$ 表示时间。卡尔曼滤波器用于动态系统的状态估计，能够在噪声和不确定性下提供实时信息更新。

通过上述分析，我们可以得到数据价值与信息价值之间的泛函关系式： $$ I = F(D) = g(D) + \epsilon + \sum_{i=1}^n F_i(D) + C + F(D(t)) $$ 这个关系式综合了非线性、非完备、不可逆、多尺度、上下文依赖和动态变化等特性，描述了数据到信息的转换过程及其影响因素。

数据价值与信息价值的传导机制

数据价值与信息价值之间的传导机制可以通过对泛函关系式的因变量进行微分分析来定性描述。我们将从非线性、非完备、不可逆、多尺度、上下文依赖和动态变化等特性出发，探讨数据到信息的转换过程及其影响因素。

1. 非线性传导机制： 数据到信息的转换过程通常是非线性的。假设 $I = g(D)$，其中 $g$ 是一个非线性函数。通过对 $D$ 进行微分，我们可以得到信息变化率与数据变化率之间的关系： $$ \frac{dI}{dD} = \nabla g(D) $$ 其中，$\nabla g(D)$ 是 $g$ 的梯度。非线性传导机制表明，数据的微小变化可能导致信息的显著变化，反之亦然。

2. 非完备性传导机制： 数据的不完备性会影响信息的提取精度。假设数据 $D$ 包含噪声 $\epsilon$，则有 $D = D_{\text{true}} + \epsilon$。根据 Cramér-Rao 不等式，估计量的方差有下界： $$ \text{Var}(\hat{\theta}) \geq \frac{1}{I(\theta)} $$ 这表明在不完备数据下，信息的提取精度受到限制。非完备性传导机制强调了数据质量对信息价值的影响。

3. 不可逆性传导机制： 数据到信息的转换过程通常是不可逆的。假设 $F$ 是一个不可逆映射，则存在信息丢失。根据 Pythagorean 定理，KL 散度在正交投影过程中满足： $$ D_{KL}(q | p) = D_{KL}(q | r) + D_{KL}(r | p) $$ 这表明信息的丢失是不可避免的。不可逆性传导机制揭示了在数据处理和转换过程中，信息丢失对信息价值的影响。

4. 多尺度传导机制： 信息可以在不同的尺度上进行分析。假设 $I = \sum_{i=1}^n F_i(D)$，其中 $F_i$ 表示在第 $i$ 个尺度上的信息提取。通过对 $D$ 进行微分，我们可以得到多尺度信息变化率： $$ \frac{dI}{dD} = \sum_{i=1}^n \frac{dF_i(D)}{dD} $$ 多尺度传导机制表明，不同尺度上的信息提取共同影响信息价值。

5. 上下文依赖性传导机制： 信息的价值依赖于其上下文。假设 $I = F(D, C)$，其中 $C$ 表示上下文信息。通过对 $D$ 和 $C$ 进行微分，我们可以得到信息变化率与数据和上下文变化率之间的关系： $$ \frac{dI}{dD} = \frac{\partial F(D, C)}{\partial D}, \quad \frac{dI}{dC} = \frac{\partial F(D, C)}{\partial C} $$ 上下文依赖性传导机制强调了上下文信息对信息价值的影响。

6. 动态性传导机制： 信息是动态变化的。假设 $I(t) = F(D(t))$，其中 $t$ 表示时间。通过对 $t$ 进行微分，我们可以得到信息变化率与时间变化率之间的关系： $$ \frac{dI(t)}{dt} = \frac{dF(D(t))}{dt} $$ 动态性传导机制表明，数据和信息随时间的变化共同影响信息价值。

范畴论的视角

范畴论（Category Theory）是数学的一个分支，研究数学结构及其之间的关系。范畴论提供了一种统一的语言和框架，用于描述和分析不同数学对象之间的关系。以下是范畴论的一些基本概念：

1. 范畴（Category）：

   • 一个范畴由对象（Objects）和态射（Morphisms）组成。对象可以是任何数学结构，如集合、向量空间等。态射是对象之间的映射，表示对象之间的关系。一个范畴 $\mathcal{C}$ 可以表示为 $\mathcal{C} = (Ob(\mathcal{C}), Hom(\mathcal{C}))$，其中 $Ob(\mathcal{C})$ 是对象的集合，$Hom(\mathcal{C})$ 是态射的集合。

2. 态射（Morphism）：

   • 态射是对象之间的映射。对于范畴 $\mathcal{C}$ 中的两个对象 $A$ 和 $B$，态射 $f: A \rightarrow B$ 表示从对象 $A$ 到对象 $B$ 的映射。态射需要满足结合律和单位元性质。

3. 函子（Functor）：

   • 函子是范畴之间的映射。一个函子 $F: \mathcal{C} \rightarrow \mathcal{D}$ 将范畴 $\mathcal{C}$ 中的对象和态射映射到范畴 $\mathcal{D}$ 中的对象和态射。函子需要保持态射的组合和单位元。

4. 自然变换（Natural Transformation）：

   • 自然变换是两个函子之间的变换。设 $F, G: \mathcal{C} \rightarrow \mathcal{D}$ 是两个从范畴 $\mathcal{C}$ 到范畴 $\mathcal{D}$ 的函子，自然变换 $\eta: F \Rightarrow G$ 是一个将 $\mathcal{C}$ 中的每个对象 $X$ 映射到 $\mathcal{D}$ 中的态射 $\eta_X: F(X) \rightarrow G(X)$ 的集合，并且对于 $\mathcal{C}$ 中的每个态射 $f: X \rightarrow Y$，有 $G(f) \circ \eta_X = \eta_Y \circ F(f)$。

数据价值与信息价值的范畴关系

在范畴论的框架下，我们可以将数据价值和信息价值视为两个范畴，并研究它们之间的关系。

1. 数据范畴与信息范畴：

   • 设 $\mathcal{D}$ 是数据范畴，其对象是数据集，态射是数据处理过程。设 $\mathcal{I}$ 是信息范畴，其对象是信息集，态射是信息处理过程。

2. 数据到信息的函子：

   • 我们可以定义一个从数据范畴 $\mathcal{D}$ 到信息范畴 $\mathcal{I}$ 的函子 $F: \mathcal{D} \rightarrow \mathcal{I}$。这个函子将数据集映射到信息集，并将数据处理过程映射到信息处理过程。具体来说，对于数据范畴中的对象 $D$ 和态射 $f: D_1 \rightarrow D_2$，函子 $F$ 将其映射为信息范畴中的对象 $I = F(D)$ 和态射 $F(f): F(D_1) \rightarrow F(D_2)$。

3. 信息价值的自然变换：

   • 设 $G, H: \mathcal{D} \rightarrow \mathcal{I}$ 是两个从数据范畴到信息范畴的函子，表示不同的信息提取方法。自然变换 $\eta: G \Rightarrow H$ 表示在不同信息提取方法之间的转换。对于数据范畴中的每个对象 $D$，自然变换 $\eta_D: G(D) \rightarrow H(D)$ 表示从信息提取方法 $G$ 到信息提取方法 $H$ 的转换过程。

4. 范畴关系的意义：

   • 通过范畴论的框架，我们可以系统地分析数据价值与信息价值之间的关系。数据到信息的转换过程可以视为范畴之间的函子映射，而不同信息提取方法之间的转换可以视为自然变换。范畴论提供了一种统一的语言，用于描述和分析数据价值与信息价值之间的传导机制。

数据价值与信息价值的对偶性

• 在范畴论中，对偶性（Duality）是一个重要概念。对于每一个范畴 $\mathcal{C}$，我们可以定义一个对偶范畴 $\mathcal{C}^{op}$，其对象与 $\mathcal{C}$ 相同，但态射的方向相反。我们可以将数据价值与信息价值视为对偶范畴，表示数据处理与信息提取过程的对偶关系。

• 设 $\mathcal{D}$ 是数据范畴，其对象是数据集，态射是数据处理过程。设 $\mathcal{I}$ 是信息范畴，其对象是信息集，态射是信息处理过程。我们可以定义数据范畴 $\mathcal{D}$ 的对偶范畴 $\mathcal{D}^{op}$，其对象与 $\mathcal{D}$ 相同，但态射的方向相反。类似地，我们可以定义信息范畴 $\mathcal{I}$ 的对偶范畴 $\mathcal{I}^{op}$。

• 对于数据范畴 $\mathcal{D}$ 和信息范畴 $\mathcal{I}$，我们可以定义一个对偶函子 $F^{op}: \mathcal{D}^{op} \rightarrow \mathcal{I}^{op}$，将数据范畴的对偶映射到信息范畴的对偶。具体来说，对于数据范畴中的对象 $D$ 和态射 $f: D_1 \rightarrow D_2$，对偶函子 $F^{op}$ 将其映射为信息范畴中的对象 $I = F(D)$ 和态射 $F^{op}(f): F(D_2) \rightarrow F(D_1)$。

• 设 $G, H: \mathcal{D} \rightarrow \mathcal{I}$ 是两个从数据范畴到信息范畴的函子，表示不同的信息提取方法。我们可以定义对偶自然变换 $\eta^{op}: G^{op} \Rightarrow H^{op}$，表示在不同信息提取方法之间的对偶转换。对于数据范畴中的每个对象 $D$，对偶自然变换 $\eta^{op}_D: G^{op}(D) \rightarrow H^{op}(D)$ 表示从信息提取方法 $G$ 到信息提取方法 $H$ 的对偶转换过程。

通过对偶范畴和对偶函子的定义，我们可以进一步分析数据价值与信息价值之间的对偶关系。数据处理过程与信息提取过程可以视为对偶范畴之间的映射，而不同信息提取方法之间的对偶转换可以视为对偶自然变换。对偶性提供了一种新的视角，用于理解数据价值与信息价值之间的相互关系。

数据价值起源于信息价值的范畴论解释

在范畴论的框架下，我们可以通过分析数据范畴和信息范畴之间的关系，来解释数据价值起源于信息价值的原因。从范畴论的视角，我们可以将数据和信息视为两个不同的范畴，通过它们之间的函子关系来理解数据价值为什么源于信息价值。

数据范畴与信息范畴

设 $\mathcal{D}$ 为数据范畴，其中对象是数据集，态射是数据处理过程。设 $\mathcal{I}$ 为信息范畴，其中对象是信息集，态射是信息处理过程。数据范畴和信息范畴之间存在一个函子 $F: \mathcal{D} \rightarrow \mathcal{I}$，将数据映射到信息。

具体而言，对于数据范畴中的对象 $D$ 和态射 $f: D_1 \rightarrow D_2$，函子 $F$ 将其映射为信息范畴中的对象 $I = F(D)$ 和态射 $F(f): F(D_1) \rightarrow F(D_2)$。这个函子保持了范畴的结构，即：

$$F(g \circ f) = F(g) \circ F(f)$$ $$F(id_D) = id_{F(D)}$$

数据价值的函子表示

数据的价值可以通过其在信息范畴中的像来度量。设 $V_\mathcal{I}$ 是信息范畴中的价值函数，则数据的价值可以表示为：

$$V_\mathcal{D}(D) = V_\mathcal{I}(F(D))$$

这个等式揭示了一个重要事实：数据的价值是通过其携带的信息来体现的。数据本身并不直接产生价值，而是通过转化为信息才获得价值。

自然变换与价值传递

设 $G, H: \mathcal{D} \rightarrow \mathcal{I}$ 是两个不同的信息提取函子，表示不同的数据分析方法。它们之间存在自然变换 $\eta: G \Rightarrow H$，对于每个数据对象 $D$，都有一个态射 $\eta_D: G(D) \rightarrow H(D)$，满足自然性条件：

$$H(f) \circ \eta_{D_1} = \eta_{D_2} \circ G(f)$$

这个自然变换描述了不同信息提取方法之间的价值转换关系。

伴随函子与价值对偶

在某些情况下，存在从信息范畴到数据范畴的函子 $U: \mathcal{I} \rightarrow \mathcal{D}$，与 $F$ 构成伴随对 $(F \dashv U)$。这意味着对于任意数据对象 $D$ 和信息对象 $I$，存在双射：

$$Hom_\mathcal{I}(F(D), I) \cong Hom_\mathcal{D}(D, U(I))$$

这种伴随关系揭示了数据价值和信息价值之间的对偶性。

价值的普遍性

数据到信息的转换过程可以看作是一个普遍构造。对于数据对象 $D$，其在信息范畴中的像 $F(D)$ 是最优的信息表示，这种最优性体现在：对于任何其他信息对象 $I$ 和从 $D$ 到 $U(I)$ 的态射 $f$，存在唯一的态射 $\tilde{f}: F(D) \rightarrow I$ 使得下图交换：

$$ \begin{CD} D @>f>> U(I) \ @V\eta_DVV @AA\epsilon_IA \ U(F(D)) @>U(\tilde{f})>> U(I) \end{CD} $$

这个普遍性质说明，数据的价值是通过其最优信息表示来实现的。通过范畴论的视角，我们可以看到，数据价值源于其携带的信息，不同的信息提取方法对应不同的价值实现路径，数据价值和信息价值之间存在对偶关系，数据的最优价值通过其普遍性质来体现。

实际例子：电子商务中的数据价值

为了更好地理解范畴论视角下的数据价值，我们可以结合电子商务中的实际例子来印证前面的几个发现。

数据范畴与信息范畴

在电子商务中，数据范畴 $\mathcal{D}$ 可以表示为用户行为数据集，例如浏览记录、购买记录等。信息范畴 $\mathcal{I}$ 则可以表示为从这些数据中提取出的有用信息，例如用户偏好、购买倾向等。函子 $F: \mathcal{D} \rightarrow \mathcal{I}$ 将用户行为数据映射为用户偏好信息。

具体而言，对于数据范畴中的对象 $D$（例如某用户的浏览记录）和态射 $f: D_1 \rightarrow D_2$（例如从一个用户的浏览记录到另一个用户的浏览记录的映射），函子 $F$ 将其映射为信息范畴中的对象 $I = F(D)$（例如用户的购买倾向）和态射 $F(f): F(D_1) \rightarrow F(D_2)$（例如从一个用户的购买倾向到另一个用户的购买倾向的映射）。

数据价值的函子表示

在电子商务中，数据的价值可以通过其在信息范畴中的像来度量。设 $V_\mathcal{I}$ 是信息范畴中的价值函数，例如用户购买倾向的商业价值，则数据的价值可以表示为：

$$V_\mathcal{D}(D) = V_\mathcal{I}(F(D))$$

这个等式揭示了一个重要事实：用户行为数据的价值是通过其转化为用户购买倾向信息来体现的。用户行为数据本身并不直接产生价值，而是通过转化为有用的信息才获得价值。

自然变换与价值传递

在电子商务中，不同的数据分析方法可以看作是不同的信息提取函子。设 $G, H: \mathcal{D} \rightarrow \mathcal{I}$ 是两个不同的信息提取函子，表示不同的数据分析方法，例如基于协同过滤和基于内容推荐的方法。它们之间存在自然变换 $\eta: G \Rightarrow H$，对于每个数据对象 $D$（例如某用户的浏览记录），都有一个态射 $\eta_D: G(D) \rightarrow H(D)$，满足自然性条件：

$$H(f) \circ \eta_{D_1} = \eta_{D_2} \circ G(f)$$

这个自然变换描述了不同信息提取方法之间的价值转换关系。例如，基于协同过滤的方法可以通过自然变换转换为基于内容推荐的方法，从而实现不同推荐方法之间的价值传递。

伴随函子与价值对偶

在某些情况下，存在从信息范畴到数据范畴的函子 $U: \mathcal{I} \rightarrow \mathcal{D}$，与 $F$ 构成伴随对 $(F \dashv U)$。这意味着对于任意用户行为数据对象 $D$ 和用户偏好信息对象 $I$，存在双射：

$$Hom_\mathcal{I}(F(D), I) \cong Hom_\mathcal{D}(D, U(I))$$

这种伴随关系揭示了用户行为数据价值和用户偏好信息价值之间的对偶性。例如，通过用户行为数据可以推断出用户的购买倾向，反之，通过用户的购买倾向也可以推断出其行为数据。

价值的普遍性

在电子商务中，用户行为数据到用户偏好信息的转换过程可以看作是一个普遍构造。对于用户行为数据对象 $D$，其在信息范畴中的像 $F(D)$ 是最优的信息表示，这种最优性体现在：对于任何其他用户偏好信息对象 $I$ 和从 $D$ 到 $U(I)$ 的态射 $f$，存在唯一的态射 $\tilde{f}: F(D) \rightarrow I$ 使得下图交换：

$$ \begin{CD} D @>f>> U(I) \ @V\eta_DVV @AA\epsilon_IA \ U(F(D)) @>U(\tilde{f})>> U(I) \end{CD} $$

第三章 数据价值的度量

从数据资产的角度来看，数据价值的度量是数据资产定价的核心问题。

3.1 度量的基本概念

在数学中，度量（Metric）是一个函数，用于定义集合中元素之间的距离。度量满足以下三个条件：

1. 非负性（Non-negativity）：对于任意两个元素 $x$ 和 $y$，度量 $d(x, y)$ 总是非负的，即 $d(x, y) \geq 0$，并且当且仅当 $x = y$ 时，$d(x, y) = 0$。

2. 对称性（Symmetry）：对于任意两个元素 $x$ 和 $y$，度量 $d(x, y)$ 满足对称性，即 $d(x, y) = d(y, x)$。

3. 三角不等式（Triangle Inequality）：对于任意三个元素 $x$、$y$ 和 $z$，度量 $d(x, y)$ 满足三角不等式，即 $d(x, z) \leq d(x, y) + d(y, z)$。

满足上述条件的函数 $d: X \times X \rightarrow \mathbb{R}$ 被称为度量，其中 $X$ 是一个集合。度量空间（Metric Space）是指一个集合 $X$ 连同其上的度量 $d$ 组成的二元组 $(X, d)$。

常见的数学度量

1. 欧式距离（Euclidean Distance）：

   • 欧式距离是最常见的度量，用于计算两个点之间的直线距离。对于两个点 $x = (x_1, x_2, \ldots, x_n)$ 和 $y = (y_1, y_2, \ldots, y_n)$，欧式距离定义为： $$ d(x, y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2} $$

2. 曼哈顿距离（Manhattan Distance）：

   • 曼哈顿距离也称为城市街区距离，用于计算两个点之间的路径距离。对于两个点 $x = (x_1, x_2, \ldots, x_n)$ 和 $y = (y_1, y_2, \ldots, y_n)$，曼哈顿距离定义为： $$ d(x, y) = \sum_{i=1}^n |x_i - y_i| $$

3. 切比雪夫距离（Chebyshev Distance）：

   • 切比雪夫距离用于计算两个点之间的最大坐标差。对于两个点 $x = (x_1, x_2, \ldots, x_n)$ 和 $y = (y_1, y_2, \ldots, y_n)$，切比雪夫距离定义为： $$ d(x, y) = \max_{i} |x_i - y_i| $$

4. 余弦相似度（Cosine Similarity）：

   • 余弦相似度用于衡量两个向量之间的相似性。对于两个向量 $x$ 和 $y$，余弦相似度定义为： $$ \text{cosine_similarity}(x, y) = \frac{x \cdot y}{|x| |y|} $$ 其中，$x \cdot y$ 表示向量的点积，$|x|$ 和 $|y|$ 表示向量的范数。

5. 马氏距离（Mahalanobis Distance）：

   • 马氏距离用于衡量数据点与数据集中心之间的距离，考虑了数据的协方差。对于���据点 $x$ 和 $y$，马氏距离定义为： $$ d(x, y) = \sqrt{(x - y)^T S^{-1} (x - y)} $$ 其中，$S$ 是数据的协方差矩阵。

6. 汉明距离（Hamming Distance）：

   • 汉明距离用于计算两个等长字符串之间不同字符的个数。对于两个字符串 $x$ 和 $y$，汉明距离定义为： $$ d(x, y) = \sum_{i=1}^n \delta(x_i, y_i) $$ 其中，$\delta(x_i, y_i)$ 当 $x_i \neq y_i$ 时为1，否则为0。

7. 黎曼度量（Riemannian Metric）：

   • 黎曼度量用于定义流形上的距离。设 $\mathcal{M}$ 是一个流形，$g$ 是定义在 $\mathcal{M}$ 上的度量张量，对于流形上的两个切向量 $u$ 和 $v$，黎曼度量定义为： $$ g(u, v) = \sum_{i,j} g_{ij} u^i v^j $$ 其中，$g_{ij}$ 是度量张量的分量。

8. 贝蒂数（Betti Numbers）：

   • 贝蒂数用于度量拓扑空间的同调特征。第 $k$ 个贝蒂数 $\beta_k$ 表示拓扑空间中 $k$ 维孔洞的数量。贝蒂数可以通过计算持续同调群得到。

度量学习（Metric Learning）

除了上述可以用数学公式直接表示的度量，还有许多复杂的度量只能通过度量学习（Metric Learning）来找到。度量学习是一种机器学习方法，旨在从数据中学习一个合适的度量函数，使得在该度量下，相似的数据点距离更近，不相似的数据点距离更远。度量学习在图像识别、自然语言处理和推荐系统等领域有广泛的应用。

1. 度量学习的基本概念：

   • 度量学习的目标是学习一个映射函数 $f: \mathcal{X} \rightarrow \mathcal{Y}$，其中 $\mathcal{X}$ 是输入空间，$\mathcal{Y}$ 是特征空间。在特征空间中，定义一个度量函数 $d: \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}$，使得对于相似的样本对 $(x_i, x_j)$，$d(f(x_i), f(x_j))$ 较小；对于不相似的样本对 $(x_i, x_k)$，$d(f(x_i), f(x_k))$ 较大。

2. 常见的度量学习方法：

   • 有监督度量学习：利用带标签的数据进行度量学习。常见的方法包括：

     • 大边界最近邻（Large Margin Nearest Neighbor, LMNN）：通过优化目标函数，使得相似样本对的距离尽可能小，不相似样本对的距离尽可能大。
     • 对比损失（Contrastive Loss）：通过最小化相似样本对的距离和最大化不相似样本对的距离来学习度量函数。
     • 三元组损失（Triplet Loss）：通过最小化三元组 $(anchor, positive, negative)$ 中锚点和正样本的距离，最大化锚点和负样本的距离来学习度量函数。

   • 无监督度量学习：利用无标签的数据进行度量学习。常见的方法包括：

     • 自编码器（Autoencoder）：通过将数据编码到低维空间，并在低维空间中定义度量函数。
     • 生成对抗网络（Generative Adversarial Network, GAN）：通过生成器和判别器的对抗训练，学习数据的潜在表示和度量函数。

3. 度量学习的应用：

   • 图像识别：在图像识别任务中，度量学习可以用于学习图像的特征表示，使得相似的图像在特征空间中距离更近，从而提高识别准确率。
   • 自然语言处理：在自然语言处理任务中，度量学习可以用于学习文本的嵌入表示，使得相似的文本在嵌入空间中距离更近，从而提高文本分类和检索的效果。
   • 推荐系统：在推荐系统中，度量学习可以用于学习用户和物品的表示，使得相似的用户和物品在特征空间中距离更近，从而提高推荐的准确性。

4. 度量学习的挑战：

   • 数据标注：有监督度量学习需要大量的标注数据，而标注数据的获取成本较高。
   • 模型复杂度：度量学习模型通常较为复杂，需要大量的计算资源和时间进行训练。
   • 泛化能力：度量学习模型在训练数据上��表现不一定能很好地泛化到测试数据，需要进行模型选择和正则化。

数据集价值与度量的关系

在数据分析和机器学习中，度量是用于衡量数据点之间相似性或差异性的工具。度量的选择直接影响到数据集的分析结果和价值评估。如果一个数据集没有找到任何合适的度量，那么其价值也就无法定义。这一现象可以通过以下数学原理来解释：

1. 度量空间的定义：

   • 在数学中，度量空间 $(X, d)$ 是一个集合 $X$ 和一个度量函数 $d: X \times X \rightarrow \mathbb{R}$ 的组合。度量函数 $d$ 满足非负性、对称性和三角不等式等性质。度量空间为数据分析提供了一个框架，使得我们可以在集合 $X$ 中定义距离和相似性。

2. 度量的存在性与数据结构：

   • 度量的存在性依赖于数据集的内在结构。如果数据集没有找到合适的度量，意味着我们无法在数据点之间定义合理的距离或相似性。这将导致数据集在度量空间中无法表示，从而无法进行进一步的数学分析和处理。

3. 度量与数据价值的关系：

   • 数据价值的量化依赖于度量函数。例如，信息熵、流形复杂度和拓扑特征等数据价值的度量方法都需要基于特�����度量函数。如果没有合适的度量函数，这些方法将无法应用，数据的价值也就无法量化。

4. 度量的选择与数据分析：

   • 在数据分析中，度量的选择直接影响到聚类、分类和回归等任务的结果。如果没有合适的度量函数，我们将无法有效地进行数据分析，导致数据的潜在价值无法挖掘和利用。

5. 度量的不可定义性与数据的无序性：

   • 如果一个数据集没有找到任何合适的度量，可能意味着数据集是无序的或随机的。在这种情况下，数据点之间没有明确的关系或模式，导致数据集无法在度量空间中表示，其价值也就无法定义。

因此，度量在数据分析和价值评估中起着至关重要的作用。如果一个数据集没有找到任何合适的度量，那么其价值也就无法定义。这一现象反映了度量在量化数据价值中的基础性作用，以及度量空间在数据分析中的重要性。

度量在量化数据价值和信息价值中的作用

度量在量化数据价值和信息价值中起着至关重要的作用。通过定义适当的度量函数，我们可以将抽象的数据和信息价值具体化，便于分析和比较。以下是度量在量化数据价值和信息价值中的几个关键作用：

1. 量化��确定性：

   • 信息熵是度量数据集不确定性的重要工具。通过计算数据集的熵值，我们可以量化数据中包含的信息量。信息熵越高，数据的不确定性越大，包含的信息量也越多。反之，信息熵越低，数据的不确定性越小，包含的信息量也越少。

2. 衡量数据间的相似性和差异性：

   • 度量函数可以用来衡量不同数据集或数据点之间的相似性和差异性。例如，欧几里得距离、曼哈顿距离和余弦相似度等度量函数可以帮助我们比较数据点之间的距离，从而识别出相似的数据点或聚类。

3. 评估数据的内在结构：

   • 流形几何中的度量工具，如测地线距离和黎曼曲率，可以帮助我们评估数据在流形上的内在结构。通过分析数据的几何特征，我们可以揭示数据的复杂性和潜在模式，从而更好地理解数据的价值。

4. 分析数据的拓扑特征：

   • 拓扑数据分析（TDA）中的度量工具，如贝蒂数和持续同调群，可以帮助我们分析数据的拓扑特征。通过度量数据的拓扑复杂度，我们可以识别出数据中的全局结构和局部模式，从而更全面地评估数据的价值。

5. 构建综合价值度量框架：

   • 通过结合信息熵、流形几何和拓扑特征等多个维度的度量工具，我们可以构建一个综合的数据价值度量框架。这个框架可以同时考虑数据的信息量、几何结构和拓扑特征，从而提供一个全面、可计算和可解释的数据价值评估方法。

3.2 数据价值度量的基本原理

数据价值的度量本质上是对数据所携带信息价值的量化。这种量化需要考虑以下几个关键方面：

1. 信息熵度量：数据集 $D$ 的信息熵 $H(D)$ 反映了数据的不确定性减少程度，可以作为数据价值的基础度量：

   $$H(D) = -\sum_{i} p(x_i) \log p(x_i)$$

   其中 $p(x_i)$ 是数据点 $x_i$ 的概率分布。

2. 流形复杂度：数据在流形上的分布特征反映了数据的内在结构。设 $\mathcal{M}$ 为数据流形，其复杂度可以通过以下指标度量：

   • 流形维数 $dim(\mathcal{M})$
   • 黎曼曲率 $R(\mathcal{M})$
   • 测地线距离 $d_g(x,y)$

3. 拓扑特征：数据的拓扑特征通过持续同调群来度量。设 $\beta_k$ 为第k个贝蒂数，则拓扑复杂度可表示为：

   $$C_{top}(D) = \sum_{k=0}^n \beta_k \cdot w_k$$

   其中 $w_k$ 是各维度的权重系数。

基于上述原理，我们可以构建数据价值的综合度量函数：

$$V(D) = \alpha_1 V_{info}(D) + \alpha_2 V_{geom}(D) + \alpha_3 V_{top}(D)$$

其中：

• $V_{info}(D)$ 是基于信息熵的价值度量
• $V_{geom}(D)$ 是基于流形几何的价值度量
• $V_{top}(D)$ 是基于拓扑特征的价值度量
• $\alpha_1, \alpha_2, \alpha_3$ 是相应的权重系数

这个度量框架具有以下特点：

1. 完备性：同时考虑了数据的信息量、几何结构和拓扑特征
2. 可计算性：每个分量都有明确的计算方法
3. 可解释性：度量结果具有清晰的物理意义
4. 可扩展性：框架可以根据具体应用进行调整和扩展

度量的实践考虑

在实际应用中，数据价值的度量还需要考虑以下因素：

1. 时效性：数据价值随时间衰减，可引入时间衰减函数： $$V(D,t) = V(D) \cdot e^{-\lambda t}$$

2. 稀缺性：数据的稀缺程度影响其价值，可通过市场供需关系调整： $$V_{market}(D) = V(D) \cdot S(D)$$ 其中 $S(D)$ 是稀缺性系数。

3. 质量因素：数据质量通过准确性、完整性等指标评估： $$V_{quality}(D) = V(D) \cdot Q(D)$$ 其中 $Q(D)$ 是质量评分。

通过这个多维度量框架，我们可以对数据价值进行科学、系统的评估，为数据资产定价和交易提供理论基础。。

3.3 度量在数据价值度量中的应���

接下来基于前面的讨论和建立的度量框架，来论述如何应用。我们将使用具体的数据类别实例分别来讨论：1）个人数据；2）企业数据；3）公共（政府）数据。

1. 个人数据

个人数据包括用户的行为数据、偏好数据、社交数据等。这些数据的价值度量可以通过以下几个方面来实现：

• 信息量：通过计算个人数据的信息熵来度量其信息量。例如，用户的浏览历史、购买记录等可以反映用户的兴趣和偏好，其信息熵越高，数据的价值越大。

以亚马逊、Netflix 和 Google 为实际实例，我们可以具体计算这些公司的个人数据价值。

亚马逊

亚马逊拥有大量的用户行为数据，包括浏览历史、购买记录、评论等。我们可以通过以下几个方面来计算这些数据的价值：

• 信息量：假设亚马逊某用户的浏览历史包含 $n$ 个页面，每个页面的访问概率为 $p_i$，则该用户浏览历史的信息熵为： $$H = -\sum_{i=1}^n p_i \log p_i$$ 例如，若某用户浏览了 10 个页面，每个页面的访问概率均为 0.1，则信息熵为： $$H = -10 \times 0.1 \log 0.1 = 1$$

• 几何结构：通过流形学习方法，我们可以将用户的行为数据嵌入到一个低维流��中。例如，假设用户的行为数据可以嵌入到一个 3 维流形中，其维数和曲率可以度量数据的复杂性和价值。

• 拓扑特征：亚马逊用户的社交网络可以表示为一个图，通过计算图的贝蒂数来度量其拓扑复杂性和价值。例如，假设某用户的社交网络图有 5 个连通分量和 10 个环路，则其贝蒂数为： $$\beta_0 = 5, \beta_1 = 10$$

Netflix

Netflix 拥有大量的用户偏好数据，包括观看历史、评分、评论等。我们可以通过以下几个方面来计算这些数据的价值：

• 信息量：假设 Netflix 某用户的观看历史包含 $m$ 部电影，每部电影的观看概率为 $q_i$，则该用户观看历史的信息熵为： $$H = -\sum_{i=1}^m q_i \log q_i$$ 例如，若某用户观看了 5 部电影，每部电影的观看概率均为 0.2，则信息熵为： $$H = -5 \times 0.2 \log 0.2 = 0.464$$

• 几何结构：通过流形学习方法，我们可以将用户的偏好数据嵌入到一个低维流形中。例如，假设用户的偏好数据可以嵌入到一个 2 维流形中，其维数和曲率可以度量数据的复杂性和价值。

• 拓扑特征：Netflix 用户的社交网络可以表示为一个图，通过计算图的贝蒂数来度量其拓扑��杂性和价值���例如，假设某用户的社交网络图有 3 个连通分量和 7 个环路，则其贝蒂数为： $$\beta_0 = 3, \beta_1 = 7$$

Google

Google 拥有大量的用户搜索数据、位置数据等。我们可以通过以下几个方面来计算这些数据的价值：

• 信息量：假设 Google 某用户的搜索历史包含 $k$ 个关键词，每个关键词的搜索概率为 $r_i$，则该用户搜索历史的信息熵为： $$H = -\sum_{i=1}^k r_i \log r_i$$ 例如，若某用户搜索了 8 个关键词，每个关键词的搜索概率均为 0.125，则信息熵为： $$H = -8 \times 0.125 \log 0.125 = 0.75$$

• 几何结构：通过流形学习方法，我们可以将用户的搜索数据嵌入到一个低维流形中。例如，假设用户的搜索数据可以嵌入到一个 4 维流形中，其维数和曲率可以度量数据的复杂性和价值。

• 拓扑特征：Google 用户的社交网络可以表示为一个图，通过计算图的贝蒂数来度量其拓扑复杂性和价值。例如，假设某用户的社交网络图有 4 个连通分量和 9 个环路，则其贝蒂数为： $$\beta_0 = 4, \beta_1 = 9$$

通过这些具体的计算实例，我们可以看到，基于信息量、几何结构和拓扑特征的多维度量框架可以有效地应用于不同公司的个人数据，帮助我们科学、系统地评估数据价值。

实验 以下Notebook展示了如何计算数据的信息熵、流形复杂度和拓扑特征：

由于都是采用随机生成的数据，因此，可以看到数据的价值度量结果差异不大。

采用不同的分布，可以看到度量的差异。

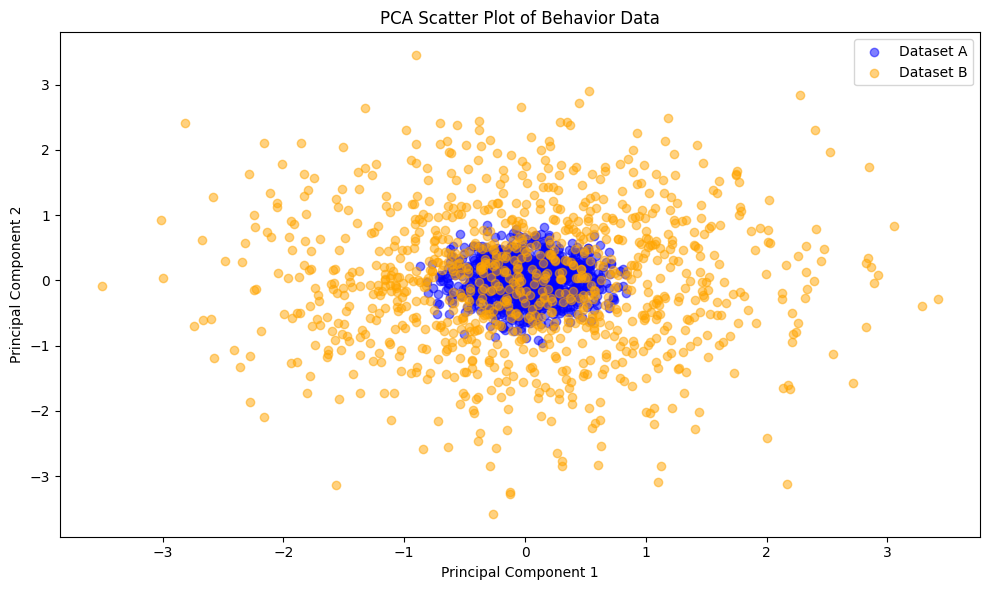
2. 企业数据

企业数据包括生产数据、销售数据、客户数据等。这些数据的价值度量可以通过以下几个方面来实现：

• 信息量：通过计算企业数据的信息熵来度量其信息量。例如，企业的销售数据可以反映市场需求和销售趋势，其信息熵越高，数据的价值越大。
• 几何结构：企业数据的几何结构可以通过流形学习方法来分析。例如，生产数据可以嵌入到一个低维流形中，通过流形的维数和曲率来度量数据的复杂性和价值。
• 拓扑特征：企业数据的拓扑特征可以通过持续同调群来分析。例如，供应链网络可以表示为一个图，通过计算图的贝蒂数来度量其拓扑复杂性和价值。

实验 以下Notebook展示了如何计算企业数据的信息熵、流形复杂度和拓扑特征：

3. 公共数据

公共数据包括气象数据、交通数据、人口数据等。这些数据的价值度量可以通过以下几个方面来实现：

• 信息量：通过计算公共数据的信息熵来度量其信息量。例如，气象数据可以反映天气变化和气候趋势，其信息熵越高，数据的价值越大。
• 几何结构：公共数据的几何结构可以通过流形学习方法来分析。例如，交通数据可以嵌入到一个低维流形中，通过流形的维数和曲率来度量数据的复杂性和价值。
• 拓扑特征：公共数据的拓扑特征可以通过持续同调群来分析。例如，人口分布可以表示为一个图，通过计算图的贝蒂数来度量其拓扑复杂性和价值。

实验 以下Notebook展示了如何计算公共数据的信息熵、流形复杂度和拓扑特征：

实验数据显示如下：

Weather Data Entropy: 1.0861632625176211e-07
Traffic Data Entropy: 6.928893407164379
Weather Data Geometry: 0.42926119924422235
Traffic Data Geometry: 0.22809012569720633
Population Network Betti 0: 1
Population Network Betti 1: 3647

3.5 范畴论视角下的数据价值度量

在范畴论框架下，数据价值的度量可以通过以下几个方面来实现：

1. 信息熵的范畴表示 设 $H: \mathcal{I} \rightarrow \mathbb{R}$ 是信息范畴上的熵函子，则数据的信息熵可表示为：

$$H_\mathcal{D}(D) = H(F(D))$$

这个熵度量反映了数据转化为信息后的不确定性减少程度。

2. 价值函子的可加性 对于数据范畴中的直和 $D_1 \oplus D_2$，价值函子满足：

$$V_\mathcal{D}(D_1 \oplus D_2) \geq V_\mathcal{D}(D_1) + V_\mathcal{D}(D_2)$$

这个不等式反映了数据组合可能产生的协同价值。

3. 信息保持度 通过考察函子 $F$ 的保真度来评估数据价值：

$$\delta(D) = \frac{\dim F(D)}{\dim D}$$

其中 $\dim$ 表示维数或信息���的某种度量。

范畴论与流形、拓扑构建的度量的联系与区别

在数据价值度量的研究中，范畴论、流形和拓扑构建提供了不同的视角和工具。它们之间既有联系也有区别。

联系

1. 抽象数学框架：

   • 范畴论、流形和拓扑构建都属于抽象数学的范畴，提供了统一的理论框架来描述和分析数据的结构和性质。
   • 这些方法都强调数据的全局结构和关系，而不仅仅是局部特征。

2. 信息的表示与转换：

   • 在范畴论中，数据通过函子从一个范畴映射到另一个范畴，信息通过自然变换在不同的函子之间传递。
   • 在流形和拓扑构建中，数据通过坐标图和同调群表示，信息通过不同尺度和视角下的拓扑特征来捕捉。

3. 度量的多样性：

   • 范畴论中的度量可以通过熵函子、价值函子和信息保持度来实现。
   • 流形和拓扑构建中的度量可以通过Fisher信息度量、KL散度和持续同调群来实现。

区别

1. 理论基础：

   • 范畴论基于对象和态射的抽象结构，强调对象之间的关系和变换。
   • 流形和拓扑构建基于几何和拓扑的概念，强调数据的空间结构和拓扑特征。

2. 应用范围：

   • 范畴论适用于广泛的数学和计算机科学领域，包括数据分析、编程语言和逻辑等。
   • 流形和拓扑构建主要应用于几何、物理和高维数据分析等领域。

3. 度量方法：

   • 范畴论中的度量方法侧重于数据的变换和信息的传递，如熵度量和价值函子。
   • 流形和拓扑构建中的度量方法侧重于数据的几何和拓扑特征，如Fisher信息度量和持续同调群。

范畴论与流形、拓扑构建在数据价值度量中提供了不同但互补的视角。范畴论强调数据的抽象关系和变换，而流形和拓扑构建则关注数据的几何和拓扑结构。通过结合这两种方法，我们可以更全面地理解和评估数据的价值。

实验 以下Notebook展示了如何计算数据的信息熵、流形复杂度和拓扑特征：

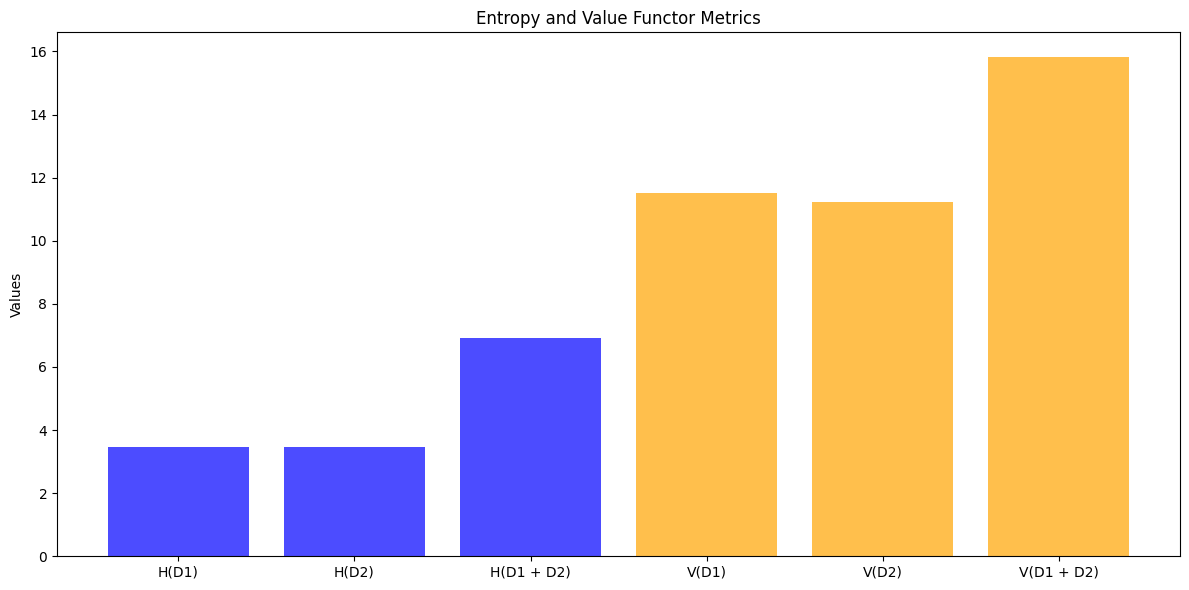
通过实验，验证范畴论度量的三个方面：信息熵、价值函子的可加性和信息保持度，并通过图表直观展示结果。

实践意义

范畴论框架在数据价值研究中��有重要的实践意义。首先，它为数据价值评估提供了坚实的理论基础。通过范畴论的数学语言，我们不仅能够严格地定义和度量数据价值，还能深入理解数据价值的来源及其传递机制。这种理论框架为数据资产的科学定价提供了可靠的数学依据，使得数据价值评估从经验判断转向了理性分析。

其次，范畴论框架能够有效指导数据处理的优化。在这个框架下，我们可以将数据处理视为范畴间的函子映射，从而系统地设计最优的数据分析流程。这种理论指导不仅适用于数据清洗和特征提取等基础工作，还能帮助我们找到实现数据价值的最优路径。通过范畴论的视角，我们能够更好地理解和优化数据处理的每个环节，确保数据价值得到最大化的实现。

最后，范畴论框架为数据资产管理提供了系统的理论支撑。它不仅为数据资产的分类提供了科学的理论基础，还能指导数据资产组合的优化策略。特别是在评估数据资产的协同效应时，范畴论的工具能够帮助我们准确把握不同数据资产之间的关系和相互作用。这使得数据资产管理从单一资产的管理提升到了整体资产组合的优化层面，为数据经济时代的资产管理提供了新的思路和方法。

3.6 量化数据集价值的起点

在前面的章节中，我们详细介绍了多种度量方法，包括欧式距离、曼哈顿距离、切比雪夫距离、余弦相似度、马氏距离、汉明距离、黎曼度量和贝蒂数等。这些度量方法为我们提供了量化数据集特征的工具，使我们能够为任何一个数据集计算出一个“量”，作为数据价值定价的起点。

度量框架的普适性

1. 多样性和灵活���：

   • 度量框架的多样性和灵活性使得我们可以根据数据集的具体特征选择合适的度量方法。例如，对于高维数据集，我们可以选择马氏距离来考虑数据的协方差；对于字符串数据集，我们可以选择汉明距离来计算不同字符的个数。
   • 这种多样性和灵活性确保了我们可以为任何类型的数据集找到合适的度量方法，从而计算出一个“量”。

2. 统一的数学基础：

   • 所有的度量方法都基于统一的数学基础，即度量空间的定义。
   • 这种统一的数学基础确保了我们可以在不同的度量方法之间进行比较和转换，从而为数据集计算出一个一致的“量”。

3. 度量学习的支持：

   • 除了传统的度量方法，度量学习（Metric Learning）为我们提供了从数据中学习合适度量函数的工具。通过度量学习，我们可以根据数据集的具体特征和任务需求，学习到一个最优的度量函数。
   • 度量学习的支持进一步增强了度量框架的普适性，使得我们可以为任何数据集计算出一个“量”。

计算“量”的过程

1. 选择合适的度量方法：

   • 根据数据集的具体特征和分析需求，选择合适的度量方法。例如，对于图像数据集，可以选择余弦相似度来衡量图像特征向量之间的相似性；对于时间序列数据集，可以选择动态时间规整（DTW）来计算时间序列之间的距离。

2. 计算度量值：

   • 选择合适的度量方法后，计算数据集中每对数据点之间的度量值。例如，对于欧式距离，可以计算每对数据点之间的直线距离；对于马氏距离，可以计算每对数据点之间的加权距离。

3. 聚合度量值：

   • 将计算得到的度量值进行聚合，得到数据集的整体度量值。例如，可以计算所有度量值的平均值、最大值或最小值，或者使用聚类算法将数据点分组，并计算每个聚类的中心点之间的距离。

数据价值定价的起点

通过上述过程，我们可以为任何一个数据集计算出一个“量”，这个“量”可以作为数据价值定价的起点。具体来说：

1. 量化数据价值：

   • 通过计算数据集的整体度量值，我们可以量化数据的相似性和差异性，从而为数据价值定价提供一个客观的基础。例如，度量值越大，数据集的多样性越高，潜在价值也越大。

2. 评估数据质量：

   • 度量值还可以用于评估数据的质量。例如，度量值越小，数据点之间的相似性越高，数据的冗余度越大，质量越低。通过评估数据质量，我们可以更准确地进行数据价值定价。

3. 指导数据处理：

   • 度量值还可以指导数据处理的优化。例如，通过分析度量值的分布，我们可以识别出数据集中的异常点和噪声，从而进行数据清洗和预处理，提高数据的质量和价值。

通过上述过程，我们可以为任何一个数据集计算出一个“量”，这个“量”可以作为数据价值定价的起点。

3.7 数据价值度量的数学证明

基于第二章对数据价值与信息价值关系的范畴论分析，我们可以严格证明为什么对数据集计算出的“量“可以作为数据价值定价的起点。

3.7.1 从范畴映射到数值映射

设 $\mathcal{D}$ 为数据范畴，$\mathcal{I}$ 为信息范畴，$F: \mathcal{D} \rightarrow \mathcal{I}$ 为从数据到信息的函子。根据前文分析，数据的价值源于其携带的信息。因此，对数据价值的度量实质上是寻找一个从数据范畴到实数的映射：

$$V: \mathcal{D} \rightarrow \mathbb{R}$$

这个映射需要满足以下性质：

1. 函子性质保持：对于数据范畴中的态射 $f: D_1 \rightarrow D_2$，有： $$V(D_2) \geq V(D_1)$$ 这反映了数据处理不会增加数据的内在价值。

2. 信息保持：存在信息范畴中的价值函数 $V_\mathcal{I}: \mathcal{I} \rightarrow \mathbb{R}$，使得： $$V(D) = V_\mathcal{I}(F(D))$$ 这保证了数据价值度量与信息价值度量的一致性。

3.7.2 价值度量的普遍构造

价值度量的构造可以通过如下步骤实现：

1. 局部度量：对数据范畴中的每个对象 $D$，通过其局部特征定义基本度量： $$V_{local}(D) = \sum_i \alpha_i m_i(D)$$ 其中 $m_i$ 是各种局部度量（如信息熵、流形维数等），$\alpha_i$ 是权重系数。

2. 全局修正：考虑数据在整个范畴中的位置： $$V_{global}(D) = V_{local}(D) \cdot \gamma(D)$$ 其中 $\gamma(D)$ 是反映数据全局特征的修正因子。

3. 价值函数的泛性质：最终的价值函数应满足泛性质，即对于任意其他满足基本性质的度量函数 $W$，存在唯一的变换 $\phi$，使得： $$W(D) = \phi(V(D))$$

3.7.3 数据价值度量的合理性

这种度量构造的理论合理性可以通过如下严格的数学证明来验证：

1. 数学一致性：通过函子 $F$ 建立的数据价值与信息价值之间的对应关系必须保持一致： $$V(D) = V_\mathcal{I}(F(D)) = \int_{\mathcal{M}} \rho(F(D)) d\mu$$ 这个等式保证了我们的度量方法与信息论的基本原理相符。

2. 稳定性保证：一个合理的度量方法应当对数据的微小变化具有稳定性。即对数据的小扰动 $\epsilon$，价值变化应当有界： $$|V(D + \epsilon) - V(D)| \leq K|\epsilon|$$ 这保证了度量结果不会因为数据的细微噪声而产生剧烈波动。

3. 可加性原理：对于独立的数据集，其价值应满足近似可加性： $$V(D_1 \cup D_2) \approx V(D_1) + V(D_2) + I(D_1; D_2)$$ 其中 $I(D_1; D_2)$ 表示两个数据集之间的信息关联度。这符合数据价值的直观认识。

4. 单调性：数据处理过程不应增加数据的内在价值： $$\text{若} \quad D_1 \xrightarrow{f} D_2, \text{则} \quad V(D_2) \leq V(D_1)$$ 这反映了信息处理不增原理。

5. 可计算性：理论必须能转化为具体的计算方法：

   • 有明确的计算步骤
   • 计算复杂度在可接受范围内
   • 结果具有数值稳定性

基于前文建立的理论框架，我们可以深入理解为什么经过合理构造的“量“能够作为数据价值定价的基础。这个问题的核心在于我们建立的数学框架与数据价值的本质特征之间存在严格的对应关系。

首先，我们构造的度量方法严格保持了数据到信息的函子映射结构。这意味着当数据通过某种处理或转换时，其价值的变化是可追踪和可预测的。通过函子的性质，我们能够确保数据处理过程中的价值传递符合信息论的基本原理。这种结构保持性为数据价值评估提供了理论保障，使得我们能够在数据流转和处理的各个环节准确追踪其价值变化。

其次，我们的度量方法满足了一系列关键的数学性质，包括稳定性、单调性和可加性。稳定性保证了对数据的微小扰动不会导致价值评估的剧烈波动；单调性确保了数据处理不会凭空产生价值；可加性则反映了数据组合的协同效应。这些数学性质共同构成了一个完整的理论框架，使得我们的价值度量方法在数学上是严格自洽的。

更重要的是，这个理论框架提供了一种系统的构造方法，能够从局部特征出发，通过严格的数学推导，最终得到反映数据整体价值的全局度量。这种从局部到全局的构造过程不是简单的叠加，而是考虑了数据内部的关联结构和整体特征。通过这种方法，我们能够捕捉到数据价值的多个层面，从而得到更全面和准确的评估结果。

最后，我们的理论具有普遍性和稳定性这两个关键特征。普遍性意味着这个理论框架可以应用于各种类型的数据和不同的应用场景；稳定性则确保了理论在实际应用中的可靠性。这两个特征使得我们的理论既有足够的适应性来处理各种实际问题，又能保持必要的稳健性以产生可靠的结果。

3.8 数据价值度量的未来展望

在数据价值度量研究中，我们目前主要运用了三种数学工具：数据流形、数据拓扑和范畴论。这些工具各自关注数据价值的不同方面，形成了互补的分析框架。

数据流形和数据拓扑提供了定量分析的基础。通过计算流形的几何特征（如维数、曲率）和拓扑不变量（如贝蒂数、持续同调），我们能够对数据的结构特征进行精确的数值度量。这些可计算的指标为数据资产定价提供了客观的量化依据。

范畴论则从更抽象的层面提供了定性分析的框架。它通过研究数据范畴之间的函子关系和自然变换，揭示了数据价值的传递机制和普遍性质。这种理论分析虽然不直接给出具体的数值，但为我们理解数据价值的本质提供了深刻的洞察。

未来数据价值度量研究的关键方向是：

1. 定量与定性的统一：

   • 建立范畴论框架下的数值计算方法
   • 将拓扑不变量与函子映射关联起来
   • 发展基于范畴论的数值优化算法

2. 多尺度分析的融合：

   • 将局部几何特征与全局拓扑性质统一起来
   • 建立跨尺度的价值传递机制
   • 发展多尺度数据价值评估方法

3. 动态价值评估：

   • 研究数据价值随时间演化的规律
   • 建立数据价值的动态预测模型
   • 发展实时数据价值评估系统

第四章 数据资产化的数学基础

在前面的章节中，基于范畴论，通过函子将信息范畴和数据范畴联系起来，并在此基础上构建了数据价值的度量框架。

我们建立了数据价值和信息价值之间的函子映射 $F: \mathcal{D} \rightarrow \mathcal{I}$，使得数据范畴 $\mathcal{D}$ 中的对象和态射可以映射到信息范畴 $\mathcal{I}$ 中。这个映射保持了基本的代数结构，使得：

$$V_\mathcal{D}(D) = V_\mathcal{I}(F(D))$$

其中 $V_\mathcal{D}$ 和 $V_\mathcal{I}$ 分别是数据价值和信息价值的度量函数。

在此基础上，我们构建了数据价值的度量框架，它包含三个关键组成部分：

1. 局部度量： $$V_{local}(D) = \sum_i \alpha_i m_i(D)$$ 其中 $m_i$ 是各种局部特征（如信息熵、流形维数等）。

2. 全局修正： $$V_{global}(D) = V_{local}(D) \cdot \gamma(D)$$ 其中 $\gamma(D)$ 反映数据在整体中的位置。

3. 时间演化： $$V(D,t) = V_{global}(D) \cdot e^{-\lambda(t)}$$ 描述了数据价值随时间的变化。

基于这些理论基础，数据资产化的数学本质可以理解为一个新的函子映射 $A: \mathcal{D} \rightarrow \mathcal{A}$，它需要同时满足：

1. 价值保持： $$V_\mathcal{A}(A(D)) = \phi(V_\mathcal{D}(D))$$ 其中 $\phi$ 是保持序的同构映射，即严格单调递增的双射函数。

2. 结构保持： $$A(f \circ g) = A(f) \circ A(g)$$ 保持数据范畴中的结构关系。

3. 可交易性： $$A(D) = \bigoplus_{i=1}^n A_i(D)$$ 使得资产可以进行分割和组合。

这种构造方式确保了数据资产既保持了原始数据的价值特征，又具备了资产所需的基本属性。特别地，通过范畴论的语言，我们可以将数据价值理论自然地扩展到资产领域：

$$ \begin{CD} \mathcal{D} @>F>> \mathcal{I} \ @VA(-)VV @VV\psi V \ \mathcal{A} @>G>> \mathcal{V} \end{CD} $$

其中 $\mathcal{V}$ 是价值范畴，这个交换图表明了数据、信息、资产和价值之间的本质关系。

基于这些理论基础，我们可以进一步探讨数据资产化的具体条件和实现机制。这不仅需要满足数学上的严格要求，还要考虑实践中的可操作性。接下来，我们将详细讨论数据资产化的必要条件和充分条件，并构建完整的框架。

4.1 数据资产化的数学定义

数据资产化是将数据转化为可度量、可交易的资产的过程。基于前文建立的数据价值理论，我们可以从范畴论的角度严格定义这个过程。

4.1.1 从价值映射到资产映射

设 $\mathcal{D}$ 为数据范畴，$\mathcal{A}$ 为资产范畴，数据资产化过程可以表示为一个函子 $A: \mathcal{D} \rightarrow \mathcal{A}$。这个资产化函子需要保持数据的价值特征，同时赋予数据资产的属性。

• $A$ 的详细定义：
  • 对象映射：对于数据范畴中的对象 $D \in \mathcal{D}$，定义 $A(D) \in \mathcal{A}$。
  • 态射映射：对于 $\mathcal{D}$ 中的态射 $f: D_1 \rightarrow D_2$，定义 $A(f): A(D_1) \rightarrow A(D_2)$，并满足：
    • 恒等映射保持：$A(\text{id}D) = \text{id}{A(D)}$。
    • 态射组合保持：$A(g \circ f) = A(g) \circ A(f)$，对于所有态射 $f: D_1 \rightarrow D_2$ 和 $g: D_2 \rightarrow D_3$。

具体而言，对于数据范畴中的对象 $D$ 和态射 $f: D_1 \rightarrow D_2$，资产化函子 $A$ 将其映射为：

• 资产范畴中的对象：$A(D)$
• 资产范畴中的态射：$A(f): A(D_1) \rightarrow A(D_2)$

这个映射需要满足以下基本性质：

1. 价值保持：设 $V_\mathcal{D}$ 和 $V_\mathcal{A}$ 分别是数据范畴和资产范畴中的价值函数，则： $$V_\mathcal{A}(A(D)) = \phi(V_\mathcal{D}(D))$$ 其中 $\phi$ 是一个保持序的同胚映射。

2. 结构保持：对于数据处理过程中的组合操作 $$A(g \circ f) = A(g) \circ A(f)$$ $$A(id_D) = id_{A(D)}$$

3. 不变量保持：数据的基本特征（如信息熵、拓扑特征等）在资产化过程中应保持不变： $$I(A(D)) = I(D)$$ 其中 $I$ 表示这些不变量。

4.1.2 资产化的基本性质

数据资产化必须满足以下四个基本性质：

1. 价值一致性： 资产的价值必须与原始数据的价值保持一致。设 $V_\mathcal{D}$ 是前文定义的数据价值度量，$V_\mathcal{A}$ 是资产价值度量，则对任意数据 $D$，存在一个保持序的同构映射 $\phi$，使得： $$V_\mathcal{A}(A(D)) = \phi(V_\mathcal{D}(D))$$ 这保证了资产化不会改变数据的内在价值。

2. 可交易性： 资产必须具有明确的边界和可分割性。对任意数据资产 $A(D)$，存在一个划分： $$A(D) = \bigoplus_{i=1}^n A_i(D)$$ 使得每个部分 $A_i(D)$ 都是可独立交易的单位。

3. 稳定性： 资产价值在时间维度上应具有相对稳定性。对时间参数 $t$，有： $$|V_\mathcal{A}(A(D), t_1) - V_\mathcal{A}(A(D), t_2)| \leq K|t_1 - t_2|$$ 其中 $K$ 是Lipschitz常数。

4. 可度量性： 资产的价值必须可以被客观度量。存在一个度量函数族 ${M_\alpha}$，使得： $$V_\mathcal{A}(A(D)) = \int_{\alpha} M_\alpha(A(D)) d\mu(\alpha)$$ 其中 $\mu$ 是适当的测度。

4.1.3 资产化的范畴论表示

在范畴论框架下，数据资产化可以表示为一个伴随函子对 $(A \dashv U)$，其中：

• $A: \mathcal{D} \rightarrow \mathcal{A}$ 是资产化函子，
• $U: \mathcal{A} \rightarrow \mathcal{D}$ 是遗忘函子

这个伴随对满足自然同构： $$Hom_\mathcal{A}(A(D), X) \cong Hom_\mathcal{D}(D, U(X))$$

这种表示揭示了数据资产化的普遍性质：对任意数据 $D$ 和资产 $X$，从 $D$ 到 $U(X)$ 的任何映射都可以唯一地提升为从 $A(D)$ 到 $X$ 的映射。这保证了资产化过程的最优性和唯一性。

4.1.4 数据资产化的普遍性质

数据资产化过程的普遍性质是一个深刻的数学特征，它通过范畴论的语言揭示了资产化过程的本质特征。让我们详细解析这个性质的含义和重要性。

普遍性质的数学表达

考虑数据范畴 $\mathcal{D}$ 中的一个数据对象 $D$ 和资产范畴 $\mathcal{A}$ 中的任意资产 $X$。资产化函子 $A$ 和遗忘函子 $U$ 之间的伴随关系可以表示为：

$$Hom_\mathcal{A}(A(D), X) \cong Hom_\mathcal{D}(D, U(X))$$

这个同构意味着存在双射：

• 从 $D$ 到 $U(X)$ 的所有可能映射
• 到 从 $A(D)$ 到 $X$ 的所有可能映射

具体而言，对于任意映射 $f: D \rightarrow U(X)$，存在唯一的映射 $\tilde{f}: A(D) \rightarrow X$ 使得下图交换：

$$ \begin{CD} D @>f>> U(X) \ @V{\eta_D}VV @AA{\epsilon_X}A \ U(A(D)) @>{U(\tilde{f})}>> U(X) \end{CD} $$

其中：

• $\eta_D$ 是单位自然变换
• $\epsilon_X$ 是余单位自然变换
• $\tilde{f}$ 是 $f$ 的唯一提升

普遍性质的实际含义

这个普遍性质有几个重要含义：

1. 最优性：

   • 资产化过程 $A(D)$ 是数据 $D$ 的最优资产表示
   • 任何其他资产化方案都可以通过 $A(D)$ 唯一地实现
   • 这保证了资产化结果的最优性

2. 唯一性：

   • 对于给定的数据 $D$，其资产化形式本质上是唯一的
   • 不同的资产化方案之间存在唯一的等价变换
   • 这确保了资产化结果的一致性

3. 普遍性：

   • 资产化过程适用于任何类型的数据
   • 可以处理各种数据到资产的转换需求
   • 提供了统一的资产化框架

4. 可逆性：

   • 通过遗忘函子 $U$，可以从资产还原出原始数据的关键特征
   • 资产化过程保持了数据的本质属性
   • 确保了资产与原始数据之间的对应关系

普遍性质的实践意义

这个普遍性质对数据资产化实践有重要指导意义：

1. 资产化方案设计：

   • 提供了评判资产化方案优劣的理论标准
   • 指导计最优的资产化转换流程
   • 帮助识别和排除次优方案

2. 资产评估体系：

   • 为建立统一的资产评估标准提供理论基础
   • 确保不同评估方法之间的一致性
   • 支持资产价值的客观度量

3. 交易机制设计：

   • 指导设计合理的资产交易规则
   • 确保交易过程中的价值保持
   • 支持灵活的资产组合和分解

通过这个普遍性质，我们不仅理解了数据资产化的数学本质，还获得了指导实践的理论工具，为数据资产化的具体实施提供了可靠的理论基础。

实验 通过一个实验来展示数据资产化的普遍性质：

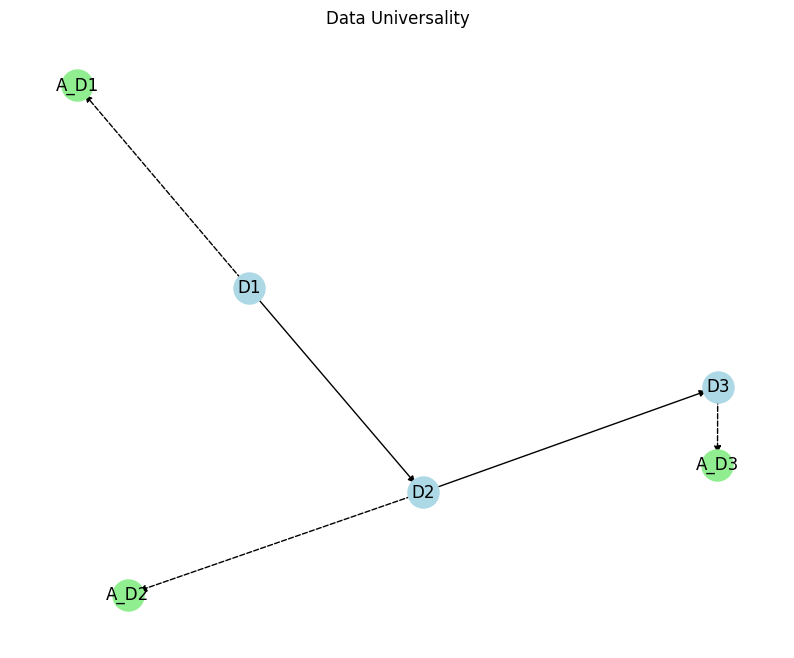
4.2 数据资产化的必要条件

数据资产化必须满足一系列必要条件，这些条件确保了资产化过程的有效性和可行性。基于前文建立的数学框架，我们可以严格定义这些必要条件。

4.2.1 价值保持条件

价值保持是数据资产化最基本的要求，它确保数据在转化为资产的过程中不会丢失其内在价值。这个条件可以通过以下数学形式来表达：

1. 信息价值的保持机制

设 $D$ 为数据对象，$A(D)$ 为其资产化形式，$I$ 为信息熵算子，则必须满足：

$$I(A(D)) \geq I(D) - \epsilon$$

其中 $\epsilon$ 是可接受的信息损失阈值。这保证了资产化过程不会显著降低数据的信息价值。

2. 数据处理过程中的价值传递

对于数据处理链 $D_1 \xrightarrow{f} D_2 \xrightarrow{g} D_3$，相应的资产价值必须满足：

$$V(A(D_3)) \leq V(A(D_1)) \cdot \eta(f,g)$$

其中 $\eta(f,g) \in (0,1]$ 表示数据处理过程的效率或价值保留率。

3. 价值累加性和协同性

对于数据集合 ${D_i}$，其资产化后的总价值应满足：

$$V(A(\cup D_i)) \geq \sum_i V(A(D_i)) + S({D_i})$$

其中 $S({D_i})$ 是协同价值项，反映了数据组合产生的额外价值。

4.2.2 一致性条件

一致性条件确保资产化过程与现有的价值评估体系相容。

1. 与已有价值度量框架的一致性

设 $V_D$ 为数据价值度量，$V_A$ 为资产价值度量，必须存在保持序的同构映射 $\phi$，使得：

$$V_A(A(D)) = \phi(V_D(D))$$

这保证了资产价值评估与据价值评估的一致性。

2. 与市场价值评估的一致性

资产价值必须反映市场供需关系：

$$V_{market}(A(D)) = V_A(A(D)) \cdot M(t)$$

其中 $M(t)$ 是市场调节因子，随时间 $t$ 变化。

3. 跨时间的价值一致性

价值评估必须满足时间一致性：

$$V_A(A(D), t_2) = V_A(A(D), t_1) \cdot e^{-\lambda(t_2-t_1)}$$

其中 $\lambda$ 是价值衰减率。

4.2.3 可操作性条件

可操作性条件确保资产化过程在实践中可以实现。

1. 资产化过程的可计算性

资产化函子 $A$ 必须是可计算的，即存在有效算法 $\mathcal{A}$，使得：

$$\forall D, \exists t < T: \mathcal{A}(D) = A(D)$$

其中 $T$ 是可接受的计算时间上限。

2. 资产边界的明确定义

资产必须具有清晰的边界定义函数 $B$：

$$B: A(D) \rightarrow {0,1}^n$$

其中 $n$ 是边界特征的维度。

3. 价值评估的可实现性

价值评估函数必须可以通过有限步骤实现：

$$V_A(A(D)) = \sum_{i=1}^k w_i \cdot m_i(A(D))$$

其中 $m_i$ 是可测量的特征，$w_i$ 是相应的权重。

这些必要条件共同构成了数据资产化的基本要求。只有同时满足这些条件，数据资产化才能既保持数据的本质价值，又具备资产的基本特征，同时在实践中可以操作实现。这些条件不仅提供了评判资产化方案的标准，也为设计资产化过程提供了指导原则。

4.3 数据资产化的充分条件

在满足必要条件的基础上，数据资产化的充分条件进一步确保了资产的完整性和可交易性。这些条件共同构成了数据资产化的完备理论框架。

4.3.1 结构完备性

结构完备性确保数据资产具有完整的数学结构，这是实现稳定价值和可交易性的基础。

1. 资产结构的数学表示

数据资产的结构可以表示为一个三元组：

$$A(D) = (S, \Phi, R)$$

其中：

• $S$ 是资产的状态空间
• $\Phi$ 是允许的操作集合
• $R$ 是关系结构

这个结构必须满足封闭性：

$$\forall \phi \in \Phi, s \in S: \phi(s) \in S$$

2. 完备性的代数特征

资产结构必须构成完备代数系统：

$$(\mathcal{A}, \oplus, \otimes, \mathcal{I}, \mathcal{U})$$

其中：

• $\oplus$ 是资产的组合操作
• $\otimes$ 是资产的复合操作
• $\mathcal{I}$ 是单位元
• $\mathcal{U}$ 是全集

满足以下公理：

• 结合律：$(a \oplus b) \oplus c = a \oplus (b \oplus c)$
• 分配律：$a \otimes (b \oplus c) = (a \otimes b) \oplus (a \otimes c)$
• 存在逆元：$\forall a, \exists a^{-1}: a \oplus a^{-1} = \mathcal{I}$

3. 拓扑完备性要求

资产空间必须构成完备度量空间：

$$(\mathcal{A}, d)$$

其中 $d$ 是满足以下条件的度量：

• 所有柯西序列都收敛
• 拓扑结构与价值函数连续相容

4.3.2 价值稳定性

价值稳定性是数据资产可持续交易的基础。

1. 时间维度的稳定性

价值函数在时间维度上满足Lipschitz条件：

$$|V(A(D), t_1) - V(A(D), t_2)| \leq K|t_1 - t_2|$$

其中 $K$ 是Lipschitz常数，表示价值变化的最大速率。

2. 市场环境的稳定性

在市场环境 $M$ 的扰动下，价值波动有界：

$$\mathbb{E}_M[|V(A(D)|M) - V(A(D))|] \leq \sigma$$

其中 $\sigma$ 是可接受的波动范围。

3. 使用场景的稳定性

对不同使用场景 $U_i$，价值评估满足：

$$V(A(D)|U_i) = V(A(D)) \cdot \gamma(U_i)$$

其中 $\gamma(U_i)$ 是场景调整因子，且：

$$\text{Var}[\gamma(U_i)] \leq \epsilon$$

4.3.3 可交易性质

可交易性是数据资产最终实现价值的关键条件。

1. 资产的可分割性

存在最小交易单位 $\delta$，使得任何资产都可以分解为：

$$A(D) = \bigoplus_{i=1}^n A_i(D)$$

其中每个 $A_i(D)$ 的粒度不小于 $\delta$，且：

$$V(A(D)) = \sum_{i=1}^n V(A_i(D)) + C({A_i})$$

其中 $C({A_i})$ 是分割成本。

2. 组合价值的协同性

对任意资产组合，存在协同价值函数 $S$：

$$V(\bigoplus_{i=1}^n A(D_i)) = \sum_{i=1}^n V(A(D_i)) + S({A(D_i)})$$

且 $S$ 满足超模性：

$$S(X \cup Y) + S(X \cap Y) \geq S(X) + S(Y)$$

3. 交易机制的数学模型

交易机制可以表示为映射 $T$：

$$T: \mathcal{A} \times \mathcal{M} \rightarrow \mathbb{R}^+ \times \mathcal{A}$$

满足以下性质：

• 价格发现：$p = T_1(A(D), M)$
• 所有权转移：$A’(D) = T_2(A(D), M)$
• 交易效率：$\text{Cost}(T) \leq \eta \cdot V(A(D))$

这些充分条件共同确保了数据资产具有：

1. 完整的数学结构
2. 稳定的价值特征
3. 可靠的交易属性

满足这些条件的数据资产化方案不仅理论上完备，而且在实践中具有可操作性，能够支持数据资产的有效流通和价值实现。

4.4 数据资产化的数学框架

基于前文讨论的必要条件和充分条件，我们可以构建一个完整的数据资产化数学框架。这个框架不仅提供了理论基础，也为实践实施提供了具体指导。

4.4.1 资产化映射的构造

资产化映射是整个框架的核心，它定义了数据如何转化为资产的具体机制。

1. 从数据范畴到资产范畴的函子

定义资产化函子 $A: \mathcal{D} \rightarrow \mathcal{A}$，它满足以下性质：

a) 对象映射：对于数据对象 $D$，有： $$A(D) = (S_D, \Phi_D, R_D, V_D)$$ 其中：

• $S_D$ 是状态空间
• $\Phi_D$ 是操作集
• $R_D$ 是关系结构
• $V_D$ 是价值函数

b) 态射映射：对于数据态射 $f: D_1 \rightarrow D_2$，有： $$A(f): A(D_1) \rightarrow A(D_2)$$ 满足交换图： $$ \begin{CD} D_1 @>f>> D_2 \ @VA(-)VV @VVA(-)V \ A(D_1) @>A(f)>> A(D_2) \end{CD} $$

2. 价值保持的数学机制

价值保持通过以下机制实现：

$$V_\mathcal{A}(A(D)) = \phi(V_\mathcal{D}(D)) + \int_{\mathcal{M}} \rho(D,m)dm$$

其中：

• $\phi$ 是基础价值映射
• $\rho(D,m)$ 是市场价值密度函数
• $\mathcal{M}$ 是市场空间

3. 资产化过程的普遍性

对任意满足条件的映射 $F: \mathcal{D} \rightarrow \mathcal{X}$，存在唯一的分解：

$$F = G \circ A$$

其中 $G: \mathcal{A} \rightarrow \mathcal{X}$ 是适当的函子。

4.4.2 资产价值的度量框架

资产价值的度量框架整合了数据价值度量和资产特有属性。

1. 继承已有的价值度量方法

基础价值度量继承自数据价值：

$$V_{base}(A(D)) = \sum_{i=1}^n \alpha_i M_i(D)$$

其中：

• $M_i$ 是第i个数据价值度量
• $\alpha_i$ 是权重系数

2. 引入资产特有的度量维度

资产特有维度通过额外的度量项引入：

$$V_{asset}(A(D)) = V_{base}(A(D)) + \sum_{j=1}^m \beta_j N_j(A(D))$$

其中：

• $N_j$ 是资产特有的度量维度
• $\beta_j$ 是相应权重

3. 构建统一的评估体系

最终的评估体系整合多个维度：

$$V_{total}(A(D)) = V_{asset}(A(D)) \cdot \gamma(t,m,u)$$

其中 $\gamma(t,m,u)$ 是综合调整因子，考虑：

• $t$: 时间因素
• $m$: 市场因素
• $u$: 使用场景

4.4.3 资产化的完备性证明

1. 必要条件的验证

对每个必要条件 $C_i$，证明：

$$\forall D \in \mathcal{D}: A(D) \text{ satisfies } C_i$$

具体包括：

• 价值保持条件：$V(A(D)) \geq V(D) - \epsilon$
• 一致性条件：$|V_1(A(D)) - V_2(A(D))| \leq \delta$
• 可操作性条件：$\exists \mathcal{A}: \text{Time}(\mathcal{A}(D)) \leq T$

2. 充分条件的证明

对充分条件集合 ${S_j}$，证明：

$$\bigwedge_j S_j \Rightarrow \text{完备的资产化过程}$$

包括：

• 结构完备性：资产结构满足代数和拓扑完备性
• 价值稳定性：价值函数满足Lipschitz条件
• 可交易性：资产具有可分割和可组合的性质

3. 框架的普适性分析

证明框架对不同类型数据的适用性：

$$\forall D \in \mathcal{D}_i: \exists! A(D) \in \mathcal{A}$$

并验证跨域一致性：

$$d(A(D_1), A(D_2)) \sim d(D_1, D_2)$$

其中 $d$ 是适当的度量。

这个数学框架通过严格的形式化定义和证明，建立了数据资产化的理论基础。它不仅满足了理论的严谨性要求，也为实践提供了可操作的指导。框架的完备性和普适性保证了它能够处理各种类型的数据资产化需求，而统一的评估体系则确保了资产价值评估的一致性和可靠性。

第五章 数据资产定价的参考模型：人类视角

5.1 数据资产定价的理论基础

数据资产定价需要建立在坚实的理论基础之上，同时考虑数据的特殊属性。本节将从传统资产定价理论出发，结合前文建立的数据价值理论，构建数据资产定价的基础框架。

5.1.1 传统资产定价理论回顾

1. 金融资产定价模型概述

传统金融资产定价主要基于以下模型：

• 资本资产定价模型(CAPM)： $$E(R_i) = R_f + \beta_i[E(R_m) - R_f]$$ 其中 $R_f$ 是无风险收益率，$\beta_i$ 是系统性风险系数。

• 套利定价理论(APT)： $$E(R_i) = R_f + \sum_{j=1}^n \beta_{ij}\lambda_j$$ 其中 $\lambda_j$ 是风险因子溢价，$\beta_{ij}$ 是敏感度系数。

2. 传统定价模型的局限性

在应用于数据资产时，传统模型存在以下局限：

• 收益的不确定性：数据资产的收益难以准确预测
• 风险度量的困难：传统的$\beta$系数难以应用
• 市场完备性缺失：数据资产市场尚不完善
• 价值传递机制差异：数据使用不遵循传统的稀缺性原则

3. 数据资产定价的特殊性

数据资产具有独特的定价特征：

• 非竞争性：多方可同时使用
• 价值递增性：使用不会损耗，可能增值
• 场景依赖性：价值随使用场景变化
• 网络外部性：价值受整体数据生态影响

5.1.2 数据价值与信息价值的映射关系

1. 价值映射函数的构造

基于前文的理论框架，构建价值映射函数：

$$V_A(D) = \phi(V_I(F(D))) + \int_{\mathcal{M}} \rho(D,m)dm$$

其中：

• $V_A(D)$ 是数据资产价值
• $V_I(F(D))$ 是信息价值
• $\phi$ 是价值转换函数
• $\rho(D,m)$ 代表市场状态变量。

2. 信息熵与价值度量

引入信息熵作为基础价值度量：

$$V_{base}(D) = \alpha H(D) + \beta I(D;Y)$$

其中：

• $H(D)$ 是数据的信息熵
• $I(D;Y)$ 是与目标变量的互信息
• $\alpha, \beta$ 是权重系数

3. 时间维度的价值演化

考虑时间因素的价值演化：

$$V(D,t) = V_{\text{info}}(D)e^{-\lambda t} + \int_0^t g(s)e^{-\lambda(t-s)}ds$$

其中：

• $\lambda$ 是基础价值衰减率
• $g(s)$ 是价值生成函数
• $r$ 是时间折现率

5.1.3 数据资产的价值组成

1. 基础信息价值

基础信息价值由数据的内在特性决定：

$$V_{info}(D) = \sum_{i=1}^n w_i m_i(D)$$

其中：

• $m_i(D)$ 是各种信息特征度量
• $w_i$ 是对应权重

2. 使用价值与潜在价值

使用价值考虑实际应用场景：

$$V_{use}(D) = \sum_{j=1}^k p_j U_j(D)$$

潜在价值考虑未来可能性：

$$V_{potential}(D) = \mathbb{E}[\sum_{t=1}^T \gamma^t V_{future}(D,t)]$$

3. 协同价值与网络效应

考虑数据组合产生的额外价值：

$$V_{synergy}(D_1,D_2) = V(D_1 \cup D_2) - V(D_1) - V(D_2)$$

网络效应通过规模函数体现：

$$V_{network}(D) = V_{base}(D) \cdot (1 + \eta(N))$$

其中 $\eta(N)$ 是网络规模效应函数。

这些理论基础为构建数据资产定价模型提供了必要的数学工具和概念框架。特别是，通过将传统金融理论与数据特有的价值特征相结合，我们可以建立更适合数据资产的定价模型。

5.2 数据资产定价模型的构建

基于前文建立的理论框架，我们现在构建一个完整的数据资产定价模型。这个模型需要同时考虑数据的内在价值特征和市场交易特性。

5.2.1 基础定价框架

1. 价值评估基准

基础定价框架采用多层次结构：

$$P(D,t) = V_{base}(D,t) \cdot \gamma(t) \cdot \delta(r)$$

其中基础价值由三个核心组件构成：

$$V_{base}(D,t) = V_{info}(D) + V_{use}(D,t) + V_{potential}(D,t)$$

(a) 信息价值组件： $$V_{info}(D) = \alpha H(D) + \beta I(D;Y) + \sum_{i=1}^n w_i m_i(D)$$

• $H(D)$：数据的信息熵
• $I(D;Y)$：与目标变量的互信息
• $m_i(D)$：其他信息特征度量

(b) 使用价值组件： $$V_{use}(D,t) = \sum_{j=1}^k p_j(t)U_j(D) \cdot (1 + \eta(N_t))$$

• $U_j(D)$：不同使用场景的价值函数
• $p_j(t)$：场景权重
• $\eta(N_t)$：网络效应函数

(c) 潜在价值组件： $$V_{potential}(D,t) = \mathbb{E}[\sum_{\tau=t+1}^T \phi(\tau-t)V_{future}(D,\tau)]$$

2. 时间折现机制

引入多因素时间折现机制：

$$\gamma(t) = e^{-(\lambda_1 + \lambda_2(t) + \lambda_3(m_t))t}$$

其中：

• $\lambda_1$：基础时间折现率
• $\lambda_2(t)$：时变折现率函数
• $\lambda_3(m_t)$：市场状态相关的折现率
• $m_t$：市场状态向量

时间价值调整满足：

$$\frac{\partial \gamma(t)}{\partial t} = -(\lambda_1 + \lambda_2’(t) + \lambda_3’(m_t)\frac{\partial m_t}{\partial t})\gamma(t)$$

3. 风险调整因子

风险调整采用多维度方法：

$$\delta(r) = \exp(-\sum_{i=1}^m \beta_i r_i)$$

其中风险因子 $r_i$ 包括：

• 数据质量风险
• 使用权限风险
• 市场流动性风险
• 技术可用性风险

风险系数 $\beta_i$ 通过以下优化问题确定：

$$\min_{\beta} \mathbb{E}[(P_{observed} - P_{model})^2] \text{ s.t. } \sum_i \beta_i = 1$$

5.2.2 多维度价值集成

1. 信息维度的价值量化

扩展信息价值度量框架：

$$V_{info}^*(D) = V_{info}(D) + \int_{\mathcal{X}} \omega(x)I(D;X=x)dx$$

其中：

• $\omega(x)$：信息价值权重函数
• $I(D;X=x)$：条件互信息

引入信息完备性度量：

$$C(D) = \frac{H(D|Y)}{H(D)} \cdot \frac{I(D;Y)}{\max_{D’} I(D’;Y)}$$

2. 使用场景的价值贡献

场景价值集成模型：

$$V_{scene}(D) = \sum_{s \in \mathcal{S}} \pi_s(t) \cdot V_s(D) \cdot (1 + \sigma_s(D))$$

其中：

• $\pi_s(t)$：场景权重函数
• $V_s(D)$：单场景价值函数
• $\sigma_s(D)$：场景协同效应函数

场景间的价值传递：

$$\frac{\partial V_s(D)}{\partial t} = \sum_{s’ \in \mathcal{S}} k_{ss’}\frac{\partial V_{s’}(D)}{\partial t}$$

3. 市场环境的影响因素

市场影响函数：

$$M(D,t) = \mu(t) \cdot \prod_{i=1}^k (1 + \theta_i(m_i(t)))$$

其中：

• $\mu(t)$：基础市场调整因子
• $\theta_i$：市场因子影响函数
• $m_i(t)$：市场指标

5.2.3 动态定价机制

1. 价值更新机制

价值动态演化方程：

$$\frac{dP(D,t)}{dt} = \alpha(t)[\hat{P}(D,t) - P(D,t)] + \sigma(t)dW_t$$

其中：

• $\hat{P}(D,t)$：目标价格
• $\alpha(t)$：调整速度
• $\sigma(t)$：波动率
• $W_t$：维纳过程

2. 市场反馈调整

引入市场反馈机制：

$$\hat{P}(D,t) = P(D,t) + \kappa(t)\sum_{i=1}^n w_i(t)[P_i^{obs}(t) - P_i^{model}(t)]$$

其中：

• $\kappa(t)$：学习率函数
• $w_i(t)$：观察权重
• $P_i^{obs}$：市场观察价格
• $P_i^{model}$：模型预测价格

3. 价格发现过程

价格发现通过迭代过程实现：

$$P_{t+1} = P_t + \eta_t \nabla L(P_t)$$

其中损失函数为：

$$L(P) = |P - V_{base}|^2 + \lambda_1 R_{market}(P) + \lambda_2 R_{smooth}(P)$$

• $R_{market}$：市场一致性正则项
• $R_{smooth}$：平滑性正则项
• $\lambda_1, \lambda_2$：正则化参数

最终的定价模型通过以下优化问题求解：

$$P^*(D,t) = \arg\min_P \mathbb{E}[L(P)] \text{ s.t. } \text{Constraints}$$

其中约束条件包括：

1. 价格非负性
2. 市场一致性
3. 时间连续性
4. 价值保持性

这个完整的定价框架既保持了理论的严谨性，又提供了实践的可操作性。通过多维度的价值集成和动态调整机制，模型能够较好地捕捉数据资产的特殊属性和市场特征。

5.3 定价模型的参数估计

基于前节构建的定���模型框架，我们需要对模型中的各类参数进行科学估计。这些参数的准确性直接影响模型的有效性。

5.3.1 基础参数的确定

1. 信息熵的计算方法

对于数据集 $D$，信息熵的计算需要考虑数据的多个维度：

(a) 离散型数据： $$H(D) = -\sum_{i=1}^n p_i \log p_i$$ 其中概率估计采用： $$p_i = \frac{count(x_i) + \alpha}{\sum_{j=1}^n count(x_j) + \alpha n}$$ 这里 $\alpha$ 是拉普拉斯平滑参数。

(b) 连续型数据： $$H(D) \approx -\int_{\mathcal{X}} f(x)\log f(x)dx \approx -\sum_{i=1}^m \hat{f}(x_i)\log \hat{f}(x_i)\Delta x$$ 其中 $\hat{f}(x)$ 通过核密度估计获得： $$\hat{f}(x) = \frac{1}{nh}\sum_{i=1}^n K(\frac{x-x_i}{h})$$

(c) 混合型数据： $$H_{mixed}(D) = \sum_{j=1}^k w_j H_j(D)$$ 其中 $w_j$ 是各类型数据的权重。

2. 时间折现率的估计

时间折现率包含多个组件：

$$\lambda_{total}(t) = \lambda_{base} + \lambda_{time}(t) + \lambda_{market}(m_t)$$

(a) 基础折现率估计： $$\lambda_{base} = r_f + \beta_D\sigma_D$$ 其中：

• $r_f$ 是无风险利率
• $\beta_D$ 是数据特征系数
• $\sigma_D$ 是数据价值波动率

(b) 时变折现率函数： $$\lambda_{time}(t) = a\cdot e^{-bt} + c$$ 参数通过历史数据拟合： $$\min_{a,b,c} \sum_{t=1}^T [\lambda_{obs}(t) - \lambda_{time}(t)]^2$$

3. 风险系数的校准

风险调整因子的参数校准：

$$\delta(r) = \exp(-\sum_{i=1}^m \beta_i r_i)$$

通过最大似然估计： $$\mathcal{L}(\beta) = \sum_{t=1}^T \log p(P_t|D_t,\beta)$$

风险系数约束： $$\sum_{i=1}^m \beta_i = 1, \beta_i \geq 0$$

5.3.2 市场参数的估计

1. 市场需求弹性

需求弹性估计模型：

$$\epsilon_D = -\frac{\partial \log Q}{\partial \log P} = -\frac{P}{Q}\frac{\partial Q}{\partial P}$$

通过回归模型估计： $$\log Q_t = \alpha - \epsilon_D \log P_t + \sum_{k=1}^K \gamma_k X_{kt} + \eta_t$$

其中：

• $Q_t$ 是需求量
• $P_t$ 是价格
• $X_{kt}$ 是控制变量
• $\eta_t$ 是误差项

2. 竞争环境影响

竞争影响函数：

$$C(D,t) = \exp(-\sum_{j=1}^n w_j d(D,D_j))$$

其中：

• $d(D,D_j)$ 是与竞争数据的距离度量
• $w_j$ 是竞争者权重

竞争强度指数： $$I_{comp}(t) = \sum_{j=1}^n \pi_j(t)\cdot s_j(t)$$ 其中：

• $\pi_j(t)$ 是竞争者市场份额
• $s_j(t)$ 是相似度系数

3. 宏观经济因素

宏观调整函数：

$$M(t) = \prod_{i=1}^k (1 + \theta_i E_i(t))$$

参数估计： $$\theta_i = \arg\min_{\theta} \sum_{t=1}^T [P_t - P_t^{model}(\theta)]^2$$

其中 $E_i(t)$ 包括：

• GDP增长率
• 通货膨胀率
• 行业景气指数
• 技术发展指数

5.3.3 场景参数的评估

1. 使用场景价值系数

场景价值函数：

$$V_s(D) = \kappa_s \cdot U_s(D) \cdot (1 + \gamma_s N_s)$$

参数估计方法： $$\kappa_s = \frac{\sum_{t=1}^T R_{st}}{\sum_{t=1}^T U_s(D_t)}$$

场景权重更新： $$\pi_s(t+1) = \pi_s(t) + \eta[\frac{R_s(t)}{R_{total}(t)} - \pi_s(t)]$$

2. 协同效应参数

协同价值函数：

$$S(D_1,D_2) = \alpha_{12}\sqrt{V(D_1)V(D_2)}\cdot I(D_1;D_2)$$

参数估计： $$\alpha_{12} = \arg\max_{\alpha} \mathcal{L}(V_{obs}|V_{model}(\alpha))$$

协同系数矩阵： $$\Sigma = [\sigma_{ij}]{n\times n}, \sigma{ij} = \text{corr}(V(D_i),V(D_j))$$

3. 网络外部性测度

网络效应函数：

$$\eta(N) = \begin{cases} a\log(1+bN), & N \leq N^* \ c + d\sqrt{N}, & N > N^* \end{cases}$$

参数估计通过分段回归： $$\min_{a,b,c,d,N^*} \sum_{t=1}^T [V_{obs}(t) - V_{base}(t)(1+\eta(N_t))]^2$$

网络价值乘数： $$\mu(N) = 1 + \eta(N) + \lambda\frac{d\eta(N)}{dN}$$

这些参数估计方法构成了完整的参数确定体系，它们共同支持定价模型的实际应用。特别注意：

1. 参数估计需要考虑数据的可获得性
2. 估计方法需要保持统计稳健性
3. 参数更新机制需要具备适应性
4. 不同参数之间的相关性需要考虑
5. 估计结果需要进行有效性验证

5.4 模型的应用与验证

在建立了完整的定价模型和参数估计方法后，我们需要通过实际应用来验证模型的有效性，并基于实践经验进行持续优化。

5.4.1 典型场景应用

1. 结构化数据定价

对于结构化数据，定价模型具体化为：

$$P_{struct}(D,t) = V_{base}(D)\cdot Q(D)\cdot T(t)\cdot M(t)$$

其中基础价值计算： $$V_{base}(D) = \sum_{i=1}^n w_i\cdot q_i\cdot v_i$$

• $q_i$：数据质量指标
• $v_i$：字段价值权重
• $w_i$：业务重要性系数

质量调整因子： $$Q(D) = \prod_{j=1}^k (1 + \alpha_j q_j(D))$$

其中 $q_j(D)$ 包括：

• 完整性：$q_c = \frac{N_{valid}}{N_{total}}$
• 准确性：$q_a = 1 - \frac{N_{error}}{N_{total}}$
• 时效性：$q_t = e^{-\lambda(t-t_0)}$

2. 非结构化数据定价

非结构化数据定价模型：

$$P_{unstruct}(D,t) = V_{content}(D)\cdot V_{format}(D)\cdot E(t)$$

内容价值评估： $$V_{content}(D) = \beta_1 H(D) + \beta_2 I(D;Y) + \beta_3 S(D)$$

其中：

• $H(D)$：信息熵
• $I(D;Y)$：目标相关性
• $S(D)$：语义丰富度

格式价值评估： $$V_{format}(D) = \sum_{k=1}^m \gamma_k F_k(D)$$

3. 实时数据流定价

实时数据流采用动态定价模型：

$$P_{stream}(D,t) = r(t)\cdot V(D,t)\cdot (1 + \delta(t))$$

实时价值函数： $$V(D,t) = \int_{t-\tau}^t v(D,s)e^{-\lambda(t-s)}ds$$

流量调整因子： $$r(t) = r_0(1 + \alpha\frac{dN(t)}{dt})$$

其中：

• $v(D,s)$：瞬时价值函数
• $N(t)$：累计数据量
• $\delta(t)$：市场波动调整

5.4.2 模型的有效性验证

1. 理论一致性检验

价值一致性验证： $$|V_{model}(D) - V_{theory}(D)| \leq \epsilon_v$$

单调性检验： $$D_1 \preceq D_2 \Rightarrow P(D_1,t) \leq P(D_2,t)$$

时间一致性： $$\frac{\partial P(D,t)}{\partial t} = -\lambda P(D,t) + f(t)$$

2. 实证效果分析

模型性能度量： $$MSE = \frac{1}{T}\sum_{t=1}^T (P_t^{obs} - P_t^{model})^2$$

预测能力评估： $$R^2 = 1 - \frac{\sum_t (P_t^{obs} - P_t^{model})^2}{\sum_t (P_t^{obs} - \bar{P}^{obs})^2}$$

稳健性检验： $$\sigma_{model} = \sqrt{\frac{1}{T-1}\sum_{t=1}^T (P_t^{model} - \bar{P}^{model})^2}$$

3. 市场反馈验证

市场接受度： $$A(t) = \frac{N_{accepted}(t)}{N_{total}(t)}$$

价格发现效率： $$E(t) = 1 - \frac{\text{Var}(P_t^{market} - P_t^{model})}{\text{Var}(P_t^{market})}$$

交易量响应： $$Q(t) = Q_0e^{-\eta|P_t^{market} - P_t^{model}|}$$

5.4.3 模型的优化与调整

1. 参数动态更新

参数更新方程： $$\theta_{t+1} = \theta_t + \alpha_t\nabla L(\theta_t)$$

学习率调整： $$\alpha_t = \frac{\alpha_0}{1 + \beta t}$$

更新频率控制： $$f_{update} = \min{f_0, \frac{1}{\sigma_{\theta}^2}}$$

2. 模型适应性改进

自适应机制： $$P_{adaptive}(D,t) = P_{base}(D,t)\cdot [1 + \phi(e_t)]$$

其中误差函数： $$e_t = P_t^{market} - P_t^{model}$$

修正函数： $$\phi(e) = \begin{cases} ke, & |e| \leq \epsilon \ \text{sign}(e)\cdot(\epsilon + \log|e/\epsilon|), & |e| > \epsilon \end{cases}$$

3. 实践经验反馈

反馈整合机制： $$F(t) = \sum_{i=1}^n w_i(t)f_i(t)$$

权重更新： $$w_i(t+1) = w_i(t) + \eta[r_i(t) - \bar{r}(t)]$$

模型调整指标： $$I_{adjust}(t) = \begin{cases} 1, & \text{if } |F(t)| > \tau \ 0, & \text{otherwise} \end{cases}$$

实践应用中需要特别注意：

1. 场景适应性

• 不同类型数据的特征提取
• 场景特定参数的调整
• 应用约束的考虑

2. 验证全面性

• 多维度的效果评估
• 长期稳定性的验证
• 异常情况的处理

3. 优化持续性

• 定期的模型评估
• 及时的参数更新
• 动态的策略调整

这个应用与验证框架确保了定价模型在实践中的有效性和可靠性，同时通过持续的优化和调整保持模型的适用性。

实验1 实验上述模型模拟计算模拟数据资产的总价值，考虑了信息熵、互信息、质量评分、使用价值、潜在价值等因素。

实验2 特征影响比较 目标: 评估不同数据特征（如信息熵、互信息、质量评分等）对数据资产总价值的影响。 步骤: 创建不同特征的数据集: 生成多个数据集，每个数据集的某个特征有显著差异。 2. 计算总价值: 使用模型计算每个数据集的总价值。 3. 比较结果: 分析不同特征对总价值的影响。

第六章 数据资产定价的参考模型：机器视角

引言

数据驱动的世界中，数据资产的定价不仅是一个经济学问题，更是一个技术挑战。传统上，人类视角在数据定价中占据主导地位，依赖于市场需求和使用场景等因素。然而，随着人工智能技术的迅猛发展，机器视角为数据定价提供了全新的方法和视角。

在前面的章节中，我们构建了一个基于数据流形、拓扑和度量框架的定价参考模型，这一模型主要体现了人类视角下的数据资产定价方法。该模型通过将数据视为嵌入在高维空间中的流形，利用拓扑结构和度量特性来评估数据的价值。人类在这一过程中依赖于对数据特征的直观理解和经验判断，结合数学工具来分析数据的复杂性和相关性。然而，这种方法在处理海量数据时，可能受到人类认知能力的限制，难以快速适应动态变化的市场环境。尽管如此，这一模型为数据定价提供了一个系统化的框架，强调了数据的内在结构和特征在价值评估中的重要性。

从人工智能和具身智能等“智能机器“的视角来看，数据价值与信息价值的联系存在显著的差异。这种差异可以通过范畴论的视角进行严格的数学描述。

设 $\mathcal{D}$ 为数据范畴，$\mathcal{I}$ 为信息范畴。在人类视角下，存在一个函子 $F: \mathcal{D} \rightarrow \mathcal{I}$，将数据映射到信息空间。这个函子通过人类的认知和理解过程，建立了数据与信息之间的对应关系。具体而言，对于数据对象 $d \in \mathcal{D}$，$F(d)$ 表示人类从数据中提取的信息。

然而，对于智能机器而言，这种映射关系发生了本质的变化。存在一个不同的函子 $G: \mathcal{D} \rightarrow \mathcal{I}$，其中包含了机器学习和动态优化的过程。关键的区别在于：

1. 自然变换的动态性： 设 $\eta: F \Rightarrow G$ 为从人类视角到机器视角的自然变换。对于任意数据对象 $d$，存在态射： $\eta_d: F(d) \rightarrow G(d)$ 这个自然变换不是静态的，而是随时间 $t$ 演化的函数族 $\eta(t)$。

2. 伴随函子的存在： 机器视角下的函子 $G$ 存在右伴随函子 $H: \mathcal{I} \rightarrow \mathcal{D}$，满足： $\text{Hom}\mathcal{I}(G(d), i) \cong \text{Hom}\mathcal{D}(d, H(i))$ 这表明机器能够通过学习建立信息到数据的反向映射，形成闭环的优化过程。

3. 张量积结构： 在机器视角下，数据范畴 $\mathcal{D}$ 上存在张量积 $\otimes$，使得对于任意数据对象 $d_1, d_2 \in \mathcal{D}$： $G(d_1 \otimes d_2) \cong G(d_1) \otimes G(d_2)$ 这反映了机器学习中的组合性和可分解性。

4. 余积结构： 对于数据对象的集合 ${d_i}{i \in I}$，存在自然同构： $G(\coprod{i \in I} d_i) \cong \coprod_{i \in I} G(d_i)$ 这描述了机器处理并行数据流的能力。

5. 单子结构： 函子组合 $T = H \circ G$ 形成一个单子 $(T, \mu, \eta)$，其中： $\mu: T^2 \rightarrow T$ $\eta: 1_\mathcal{D} \rightarrow T$ 这个代数结构刻画了机器学习中的迭代优化过程。

这种数学框架揭示了机器视角下数据-信息转换的几个核心特性：

1. 动态性质： 通过时变自然变换族 ${\eta(t)}{t \in \mathbb{R}+}$ 描述的动态映射满足： $\frac{d}{dt}\eta(t) = \mathcal{L}(\eta(t))$ 其中 $\mathcal{L}$ 是描述学习动力学的算子。

2. 优化结构： 存在目标泛函 $\mathcal{J}: \text{Nat}(F,G) \rightarrow \mathbb{R}$，使得最优自然变换满足： $\eta^* = \arg\min_{\eta} \mathcal{J}(\eta)$ 这描述了机器学习中的优化目标。

3. 信息度量： 在范畴 $\mathcal{I}$ 中存在信息度量函子 $M: \mathcal{I} \rightarrow \mathbf{Set}$，满足： $M(G(d)) = \mathcal{V}(d)$ 其中 $\mathcal{V}(d)$ 表示数据 $d$ 的价值测度。

这些数学结构共同解释了为什么机器能够在数据流动过程中实现实时评估和优化，并通过强化学习不断调整其定价策略。这种理论框架不仅提供了对机器视角的深入理解，也为设计更高效的数据定价算法提供了理论指导。

具身智能体的自主决策能力为数据定价带来了新的可能性。这些智能体通过传感器和接口与物理世界交互，获取实时数据，能够感知环境变化，并根据感知信息调整行为。通过深度学习和强化学习算法，具身智能体能够自主学习环境中的最佳行为策略。通过不断的试错和反馈，智能体能够在复杂环境中实现自我优化。

机器视角为数据资产定价提供了新的可能性。通过利用人工智能和具身智能体的强大能力，我们可以实现更高效、更精准的数据定价策略。这不仅提升了数据的经济价值，也为数据驱动的决策提供了更坚实的基础。

6.1 参考模型

基于范畴论，我们可以构建一个机器视角的数据资产定价参考模型。这个模型将智能机器的感知、学习和决策过程形式化为范畴论框架。

基本范畴结构

1. 感知范畴 $\mathcal{P}$：

• 对象：感知数据 $p \in \text{Ob}(\mathcal{P})$
• 态射：感知转换 $f: p_1 \rightarrow p_2$
• 张量积：多模态感知融合 $p_1 \otimes p_2$

2. 数据范畴 $\mathcal{D}$：

• 对象：数据资产 $d \in \text{Ob}(\mathcal{D})$
• 态射：数据转换 $g: d_1 \rightarrow d_2$
• 余积：数据聚合 $\coprod_{i \in I} d_i$

3. 价值范畴 $\mathcal{V}$：

• 对象：价值度量 $v \in \text{Ob}(\mathcal{V})$
• 态射：价值比较 $h: v_1 \rightarrow v_2$
• 序结构：$v_1 \leq v_2$

函子与自然变换

1. 感知函子 $S: \mathcal{P} \rightarrow \mathcal{D}$： $S(p)$ 表示从感知到数据的映射，满足： $S(p_1 \otimes p_2) \cong S(p_1) \otimes S(p_2)$

2. 价值评估函子 $E: \mathcal{D} \rightarrow \mathcal{V}$： $E(d)$ 表示数据的价值评估，满足： $E(\coprod_{i \in I} d_i) \cong \bigvee_{i \in I} E(d_i)$

3. 学习变换 $\eta: E \circ S \Rightarrow E’$： $\eta_p: E(S(p)) \rightarrow E’(S(p))$ 表示学习过程中价值评估的动态调整。

定价模型的数学结构

1. 价值泛函： $\mathcal{J}: \text{Ob}(\mathcal{D}) \rightarrow \mathbb{R}+$ $\mathcal{J}(d) = \int_T \text{val}(E(d,t))dt$ 其中 $\text{val}: \text{Ob}(\mathcal{V}) \rightarrow \mathbb{R}+$ 是价值度量。

2. 动态优化： 定价策略 $\pi: \mathcal{D} \times T \rightarrow \mathbb{R}+$ 满足： $\pi^*(d,t) = \arg\max{\pi} \mathbb{E}[\sum_{t’=t}^T \gamma^{t’-t}\mathcal{J}(d_{t’})]$ 其中 $\gamma$ 是折扣因子。

3. 反馈结构： 存在伴随函子对 $(F, G)$： $F: \mathcal{D} \rightarrow \mathcal{V}$ $G: \mathcal{V} \rightarrow \mathcal{D}$ 满足： $\text{Hom}\mathcal{V}(F(d), v) \cong \text{Hom}\mathcal{D}(d, G(v))$

具身智能体的定价机制

1. 状态-动作范畴 $\mathcal{A}$：

• 对象：状态-动作对 $(s,a) \in \text{Ob}(\mathcal{A})$
• 态射：状态转换 $\tau: (s_1,a_1) \rightarrow (s_2,a_2)$

2. 价值学习函子 $L: \mathcal{A} \rightarrow \mathcal{V}$： $L(s,a)$ 表示状态-动作对的价值，满足： $L(s,a) = \mathbb{E}[r + \gamma \max_{a’} L(s’,a’)]$

3. 定价策略函子 $\Pi: \mathcal{D} \times \mathcal{A} \rightarrow \mathcal{V}$： $\Pi(d,s,a)$ 表示在状态 $s$ 下对数据 $d$ 采取动作 $a$ 的价值。

这个范畴论框架具有以下特点：

1. 完备性：通过范畴、函子和自然变换完整描述了定价过程
2. 动态性：通过时变函子和自然变换捕捉了定价的动态特性
3. 反馈性：通过伴随函子对实现了价值评估的反馈优化
4. 组合性：通过张量积和余积结构支持复杂数据的处理

这个模型为机器视角下的数据资产定价提供了严格的数学基础，支持具身智能体进行自主的数据价值评估和定价决策。

6.2 人工智能模型对数据的需求

数据被视为驱动人工智能模型学习和决策的核心资源。数据的质量、数量和特征直接影响模型的性能和泛化能力。理解数据在模型训练中的价值以及数据特征对模型的影响，是构建高效人工智能系统的关键。

6.2.1 数据在模型训练中的价值

数据在人工智能模型训练中扮演着至关重要的角色。首先，数据质量与模型性能密切相关。高质量的数据通常意味着更少的噪声和错误，这使得模型能够更准确地学习数据中的模式和关系。数据质量的提升可以通过清洗、去重和纠错等方法实现，从而提高模型的准确性和可靠性。

其次，数据多样性是模型泛化能力的基础。多样化的数据集能够覆盖更广泛的输入空间，使得模型在面对未见过的数据时仍能保持良好的性能。多样性不仅体现在数据的种类和来源上，还包括数据的分布和特征。通过引入多样化的数据，模型能够更好地适应不同的应用场景，减少过拟合的风险。

此外，数据量与模型复杂度之间存在密切关系。一般来说，复杂的模型需要大量的数据来进行有效的训练，以避免过拟合。数据量的增加可以帮助模型更好地捕捉数据中的复杂模式和细节。然而，数据量的增加也带来了计算和存储的挑战，因此在实际应用中，需要在数据量和计算资源之间找到平衡。

6.2.2 数据特征对模型的影响

数据特征的选择和处理对模型的性能有着深远的影响。特征选择是指从原始数据中提取出对模型预测最有用的特征。通过特征选择，可以减少数据的维度，降低模型的复杂度，提高训练效率。特征的重要性评估可以通过统计方法和机器学习算法实现，如基于信息增益、互信息或L1正则化的特征选择方法。

数据预处理与特征工程是提高模型性能的关键步骤。数据预处理包括归一化、标准化、缺失值填补等操作，旨在消除数据中的偏差和异常。特征工程则是通过创造新的特征或转换现有特征来增强模型的学习能力。有效的特征工程可以显著提高模型的预测准确性和稳定性。

数据增强与合成数据的使用是应对数据不足和不平衡问题的有效策略。数据增强通过对现有数据进行变换（如旋转、缩放、翻转等）来生成新的样本，从而增加数据的多样性。合成数据则是通过生成模型（如GANs）来创建新的数据样本，特别是在数据获取困难或昂贵的情况下，合成数据可以为模型提供额外的训练资源。

数据在人工智能模型中的作用不可忽视。通过提高数据质量、增加数据多样性、合理选择和处理数据特征，AI系统能够更好地学习和泛化，从而在复杂的现实世界中表现出色。

6.2.3 数据与算力的协同：Scaling Law的巨大成就

在过去的几年中，Scaling Law（缩放定律）在推动ChatGPT等大型语言模型的发展中发挥了至关重要的作用。缩放定律揭示了模型性能、数据量和计算资源之间的关系，为构建更强大的人工智能系统提供了理论基础和实践指导。

1. 缩放定律的基本原理

缩放定律指出，随着模型参数数量、训练数据量和计算资源的增加，模型的性能会持续提升。具体来说，模型的误差（如语言模型中的困惑度）与模型规模、数据量和计算量之间存在幂律关系。通过增加模型参数和训练数据，可以显著提高模型的预测能力和泛化性能。

2. 数据与算力的协同效应

在ChatGPT的训练过程中，数据和算力的协同效应尤为显著。首先，大规模的高质量数据是训练强大语言模型的基础。OpenAI通过收集和清洗海量的文本数据，确保模型能够学习到丰富的语言模式和知识。数据的多样性和覆盖面直接影响模型的表现，使其能够在各种语言任务中表现出色。

其次，算力的提升为训练大规模模型提供了必要的支持。随着硬件技术的发展，特别是GPU和TPU等专用计算设备的进步，训练大规模模型所需的计算资源得到了极大提升。分布式计算技术的应用，使得训练过程可以在多个计算节点上并行进行，大大缩短了训练时间。

3. ChatGPT的成功案例

ChatGPT的成功是缩放定律在实践中的典型案例。通过不断增加模型参数和训练数据，OpenAI成功地构建了一个具有1750亿参数的超大规模语言模型。该模型在各种自然语言处理任务中表现出色，包括文本生成、问答、翻译等。

在训练过程中，OpenAI利用了大规模的计算集群和高效的分布式训练算法，确保模型能够在合理的时间内完成训练。数据与算力的协同作用，使得ChatGPT能够在理解和生成自然语言方面达到前所未有的水平。

4. 缩放定律的未来展望

缩放定律的成功应用不仅推动了ChatGPT的发展，也为未来的人工智能研究指明了方向。随着数据和算力的进一步提升，未来的语言模型将变得更加智能和强大。研究人员将继续探索更高效的训练方法和模型架构，以充分利用数据和算力的协同效应，推动人工智能技术的不断进步。

基于前面构建的范畴论框架，我们可以对Scaling Law及其边界特性进行形式化推导。

1. 范畴论框架下的Scaling特性

设定基本范畴：

• 数据范畴 $\mathcal{D}$
• 模型范畴 $\mathcal{M}$
• 性能范畴 $\mathcal{P}$

1.1 基本函子关系

1. 规模函子 $S: \mathcal{D} \times \mathcal{M} \rightarrow \mathbb{R}_+$： $S(d,m) = (|d|, |m|)$，其中 $|d|$ 和 $|m|$ 分别表示数据规模和模型参数量

2. 性能函子 $P: \mathcal{D} \times \mathcal{M} \rightarrow \mathcal{P}$： $P(d,m)$ 表示在数据集 $d$ 上模型 $m$ 的性能

3. 计算函子 $C: \mathcal{M} \times \mathcal{D} \rightarrow \mathbb{R}_+$： $C(m,d)$ 表示训练模型所需的计算资源

2. Scaling Law的形式化表达

2.1 幂律关系

对于性能度量 $L \in \text{Ob}(\mathcal{P})$，存在幂律关系：

$L(N) = \alpha N^{-\beta}$

其中：

• $N$ 是模型参数量
• $\alpha, \beta$ 是常数
• $L$ 表示损失函数值

这可以通过自然变换 $\eta: P \Rightarrow \mathbb{R}_+$ 表示：

$\eta_{d,m}: P(d,m) \rightarrow L(|m|) = \alpha |m|^{-\beta}$

2.2 计算边界

定义计算约束函子 $B: \mathcal{M} \rightarrow \mathbb{R}_+$：

$B(m) = \text{max}{C(m,d) | d \in \text{Ob}(\mathcal{D})}$

满足： $B(m) \leq K$，其中 $K$ 是可用计算资源上限

3. Scaling Law的边界特性

3.1 数据效率边界

存在自然变换 $\theta: S \Rightarrow P$，满足：

$\theta_{d,m}: S(d,m) \rightarrow L(|d|, |m|)$

其中数据效率边界由下式给出：

$\frac{\partial L}{\partial |d|} = -\gamma_d |d|^{-\delta}$

这表明性能提升的边际效应递减。

3.2 计算效率边界

定义计算效率泛函 $\mathcal{E}: \text{Ob}(\mathcal{M}) \rightarrow \mathbb{R}_+$：

$\mathcal{E}(m) = \frac{P(d,m)}{C(m,d)}$

存在最优点 $m^*$，满足：

$m^* = \arg\max_m \mathcal{E}(m)$ subject to $B(m) \leq K$

4. 协同优化定理

给定数据-模型对 $(d,m)$，存在最优缩放路径 $\gamma: [0,1] \rightarrow \mathcal{D} \times \mathcal{M}$，满足：

1. 路径优化性： $\frac{d}{dt}P(\gamma(t)) \geq 0$

2. 资源约束： $\int_0^1 C(\gamma(t))dt \leq K$

3. 边界条件： $\gamma(0) = (d_0,m_0)$ $\gamma(1) = (d^,m^)$

5. Scaling Law的极限特性

1. 渐近行为： $\lim_{|m| \rightarrow \infty} L = \alpha_{\infty}$ 其中 $\alpha_{\infty}$ 是理论最优性能

2. 计算复杂度边界： $C(m,d) = \Omega(|m| \cdot |d|)$

3. 最优缩放率： $\frac{d\log|m|}{d\log|d|} = \kappa$ 其中 $\kappa$ 是最优缩放系数

这个形式化框架揭示了Scaling Law的几个重要特性：

1. 计算效率边界：存在计算资源投入的边际效应递减
2. 数据效率边界：数据规模增长带来的性能提升存在上限
3. 协同优化性：数据规模和模型规模需要协同增长
4. 渐近行为：性能提升存在理论上限

6.3 智能体的自主定价机制

在数据驱动的经济中，智能体的自主定价机制为数据资产的动态评估和交易提供了新的可能性。通过利用先进的人工智能技术，智能体能够在复杂的市场环境中自主学习和调整定价策略，以实现最优的经济效益。

6.3.1 智能体的决策框架

智能体的决策框架是其自主定价能力的核心。强化学习作为一种重要的机器学习方法，在数据定价中发挥着关键作用。通过与环境的交互，智能体能够在试错过程中学习最优的定价策略。强化学习的目标是通过最大化累积奖励来优化智能体的行为策略。在数据定价的场景中，奖励函数可以设计为与利润、市场份额或客户满意度相关的指标。

智能体的学习策略与目标函数密切相关。学习策略决定了智能体如何探索和利用环境信息，以提高决策的有效性。常见的学习策略包括Q学习、策略梯度和深度Q网络（DQN）等。目标函数则定义了智能体在不同情境下的优先级和目标，例如在竞争激烈的市场中，智能体可能更关注市场份额的增长，而在稳定市场中则可能更关注利润的最大化。

环境感知与动态调整是智能体决策框架中的重要组成部分。智能体通过传感器和数据接口感知市场环境的变化，包括竞争对手的定价策略、市场需求的波动以及宏观经济因素的影响。基于这些感知信息，智能体能够动态调整其定价策略，以适应不断变化的市场环境。这种动态调整能力使得智能体能够在复杂的市场中保持竞争优势。

6.3.2 具身智能体的定价策略

具身智能体通过其感知与交互能力，在数据定价中展现出独特的优势。具身智能体能够通过物理传感器和网络接口获取实时数据，这些数据包括市场动态、用户行为和环境变化等。通过对这些数据的分析，具身智能体能够实时评估数据的价值，并根据市场需求和供给情况调整定价策略。

数据价值的实时评估是具身智能体定价策略的核心。具身智能体利用机器学习和数据分析技术，能够快速识别数据的潜在价值和市场机会。通过对历史数据和实时数据的综合分析，智能体能够预测市场趋势和用户需求，从而在最佳时机进行定价调整。

自主定价的反馈机制是具身智能体实现自我优化的重要手段。通过收集和分析定价决策的结果，智能体能够评估其定价策略的有效性，并根据反馈信息进行策略调整。这种反馈机制不仅提高了定价的准确性和灵活性，还使得智能体能够在不断变化的市场中持续优化其定价策略。

综上所述，智能体的自主定价机制通过强化学习、环境感知和实时评估，为数据资产的动态定价提供了强有力的支持。具身智能体的感知与交互能力进一步增强了其在复杂市场环境中的适应性和竞争力。这种自主定价机制不仅提升了数据的经济价值，也为智能体在数据驱动的经济中发挥更大作用奠定了基础。

基于范畴论框架，我们可以对智能体的自主定价机制进行形式化推导，得出一系列重要推论。

1. 基本范畴结构扩展

1.1 市场范畴 $\mathcal{M}$

• 对象：市场状态 $m \in \text{Ob}(\mathcal{M})$
• 态射：市场转换 $f: m_1 \rightarrow m_2$
• 序结构：$m_1 \preceq m_2$ 表示市场状态的偏序关系

1.2 策略范畴 $\mathcal{S}$

• 对象：定价策略 $s \in \text{Ob}(\mathcal{S})$
• 态射：策略转换 $g: s_1 \rightarrow s_2$
• 张量积：策略组合 $s_1 \otimes s_2$

2. 强化学习的范畴论表示

定义状态-动作-奖励函子 $R: \mathcal{M} \times \mathcal{S} \rightarrow \mathbb{R}$：

$R(m,s) = \mathbb{E}[\sum_{t=0}^{\infty} \gamma^t r_t]$

其中：

• $r_t$ 是即时奖励
• $\gamma$ 是折扣因子

推论 1 (最优策略存在性)

存在最优策略函子 $\Pi^*: \mathcal{M} \rightarrow \mathcal{S}$，满足：

$\Pi^*(m) = \arg\max_{s \in \text{Ob}(\mathcal{S})} R(m,s)$

3. 具身智能体的形式化

3.1 感知函子 $P: \mathcal{M} \rightarrow \mathcal{D}$

将市场状态映射到数据空间：

$P(m) = {d \in \mathcal{D} | d \text{ is observable in } m}$

3.2 价值评估函子 $V: \mathcal{D} \times \mathcal{M} \rightarrow \mathbb{R}_+$

满足以下性质：

1. 单调性： 如果 $d_1 \subseteq d_2$，则 $V(d_1,m) \leq V(d_2,m)$

2. 次模性： $V(d_1 \cup d_2,m) + V(d_1 \cap d_2,m) \leq V(d_1,m) + V(d_2,m)$

推论 2 (价值评估的边界性质)

对于任意数据集 $d \in \mathcal{D}$，存在上界：

$V(d,m) \leq \sup_{s \in \mathcal{S}} R(m,s)$

4. 动态定价机制

定义定价函子 $\Phi: \mathcal{D} \times \mathcal{M} \times \mathcal{S} \rightarrow \mathbb{R}_+$

4.1 实时更新方程

存在自然变换 $\eta: \Phi \Rightarrow \Phi’$：

$\frac{d}{dt}\Phi(d,m,s) = \eta_{d,m,s}(\nabla_s R(m,s))$

推论 3 (定价收敛性)

在适当条件下，定价序列收敛：

$\lim_{t \rightarrow \infty} \Phi_t(d,m,s) = \Phi^*(d,m)$

5. 反馈优化机制

定义反馈函子 $F: \mathcal{S} \times \mathbb{R}_+ \rightarrow \mathcal{S}$：

$F(s,r) = s’$ 其中 $s’$ 是基于奖励 $r$ 优化后的策略

推论 4 (反馈优化的单调性)

对于任意策略 $s \in \mathcal{S}$：

$R(m,F(s,r)) \geq R(m,s)$

6. 重要推论

1. 最优性定理： 在完备市场信息下，存在全局最优定价策略。

2. 适应性定理： 具身智能体的定价策略能够自适应收敛到局部最优解。

3. 稳定性定理： 在市场扰动有界的情况下，定价策略具有鲁棒性。

4. 效率定理： 反馈优化机制能够单调提升策略性能。

这些推论为智能体的自主定价机制提供了理论保证，表明：

1. 定价策略的收敛性是有保证的
2. 具身智能体能够通过感知和学习达到局部最优
3. 反馈机制能够持续改进定价策略
4. 系统具有对市场变化的适应能力

这些理论结果为设计和实现具身智能体的定价系统提供了重要指导。

6.4 数据资产的机器定价模型

1.1 定义基础范畴

1. 数据范畴 $\mathcal{D}$：

   • 对象：数据集 $d \in \text{Ob}(\mathcal{D})$
   • 态射：数据转换 $f: d_1 \rightarrow d_2$
   • 张量积：$d_1 \otimes d_2$ 表示数据融合

2. 特征范畴 $\mathcal{F}$：

   • 对象：特征空间 $f \in \text{Ob}(\mathcal{F})$
   • 态射：特征映射 $\phi: f_1 \rightarrow f_2$
   • 余积：$\coprod_{i \in I} f_i$ 表示特征组合

3. 价格范畴 $\mathcal{P}$：

   • 对象：价格空间 $p \in \text{Ob}(\mathcal{P})$
   • 态射：价格变换 $\pi: p_1 \rightarrow p_2$
   • 序结构：$(p_1 \leq p_2)$

2. 函子构造

2.1 特征提取函子

定义 $E: \mathcal{D} \rightarrow \mathcal{F}$： $E(d) = f$ 其中 $f$ 是数据 $d$ 的特征表示

2.2 定价函子

定义 $\Phi: \mathcal{F} \rightarrow \mathcal{P}$： $\Phi(f) = p$ 其中 $p$ 是特征 $f$ 对应的价格

3. 自适应机制

3.1 学习自然变换

定义 $\eta: \Phi \Rightarrow \Phi’$： $\eta_f: \Phi(f) \rightarrow \Phi’(f)$

满足动态更新方程： $\frac{d}{dt}\Phi(f) = -\eta_f \cdot \nabla_f \mathcal{J}(\Phi(f))$

其中 $\mathcal{J}$ 是目标泛函。

4. 存在性证明

定理 1 (自适应定价模型的存在性)

设 $(\mathcal{D}, \mathcal{F}, \mathcal{P})$ 为上述范畴系统，则存在唯一的自适应定价模型。

证明：

1. 构造完备度量空间： $(\mathcal{P}, d_P)$ 其中 $d_P$ 是价格空间上的度量

2. 定义压缩映射： $T: \mathcal{P} \rightarrow \mathcal{P}$ $T(p) = \Phi(E(d))$ 对任意 $d \in \mathcal{D}$

3. 验证压缩性： $d_P(T(p_1), T(p_2)) \leq \alpha d_P(p_1, p_2)$ 其中 $\alpha < 1$

4. 应用不动点定理，得到唯一解。

5. 基本性质推导

5.1 连续性定理

定理 2 (定价连续性) 对于任意数据序列 ${d_n}$，如果 $d_n \rightarrow d$，则： $\lim_{n \rightarrow \infty} \Phi(E(d_n)) = \Phi(E(d))$

证明： 利用函子的连续性和自然变换的光滑性。

5.2 最优性定理

定理 3 (局部最优性) 存在邻域 $U(d)$，使得对任意 $d’ \in U(d)$： $\mathcal{J}(\Phi(E(d))) \leq \mathcal{J}(\Phi(E(d’)))$

证明： 应用变分原理和梯度下降的收敛性。

5.3 稳定性定理

定理 4 (Lyapunov稳定性) 存在Lyapunov函数 $V: \mathcal{P} \rightarrow \mathbb{R}_+$，满足： $\frac{d}{dt}V(\Phi(E(d))) \leq 0$

6. 重要推论

推论 1 (适应性)

模型能够自适应调整以响应市场变化： $|\Phi’(f) - \Phi(f)| \leq \epsilon(t)$ 其中 $\epsilon(t) \rightarrow 0$ 当 $t \rightarrow \infty$

推论 2 (鲁棒性)

对于有界扰动 $\delta$： $|\Phi(f + \delta) - \Phi(f)| \leq K|\delta|$ 其中 $K$ 是Lipschitz常数

推论 3 (收敛速度)

在适当条件下，收敛速度为指数级： $|\Phi_t(f) - \Phi^*(f)| \leq Ce^{-\lambda t}$

7. 模型特性总结

1. 存在性：模型解的存在性和唯一性得到保证
2. 连续性：定价函数关于输入数据是连续的
3. 最优性：能够达到局部最优解
4. 稳定性：系统动力学是Lyapunov稳定的
5. 适应性：能够自适应调整以响应市场变化
6. 鲁棒性：对输入扰动具有有界响应

实验

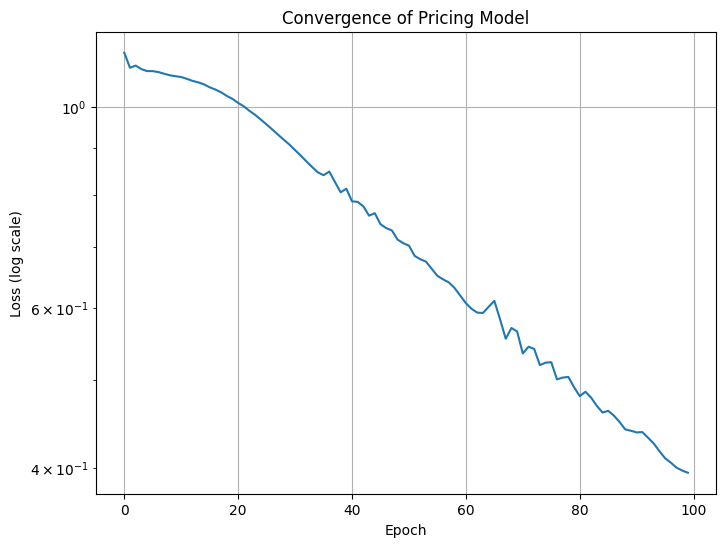
参考文献

Tenenbaum JB, de Silva V, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science. 2000 Dec 22;290(5500):2319-23. doi: 10.1126/science.290.5500.2319. PMID: 11125149.

Cohen, U., Chung, S., Lee, D.D. et al. Separability and geometry of object manifolds in deep neural networks. Nat Commun 11, 746 (2020). https://doi.org/10.1038/s41467-020-14578-5

Bradley CA Brown and Anthony L. Caterini and Brendan Leigh Ross and Jesse C Cresswell and Gabriel Loaiza-Ganem. The Union of Manifolds Hypothesis. NeurIPS 2022 Workshop on Symmetry and Geometry in Neural Representations. https://openreview.net/forum?id=aJp8UXRKvVm

Bengio Y, Courville A, Vincent P. Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013 Aug;35(8):1798-1828. doi: 10.1109/TPAMI.2013.50.

Goodfellow I, Bengio Y, Courville A. Deep Learning. MIT Press; 2016. Available from: http://www.deeplearningbook.org

Kingma DP, Welling M. Auto-Encoding Variational Bayes. arXiv preprint arXiv:1312.6114. 2013 Dec 20. Available from: https://arxiv.org/abs/1312.6114

LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015 May 28;521(7553):436-44. doi: 10.1038/nature14539.

Hinton GE, Salakhutdinov RR. Reducing the dimensionality of data with neural networks. Science. 2006 Jul 28;313(5786):504-7. doi: 10.1126/science.1127647.

Rifai S, Vincent P, Muller X, Glorot X, Bengio Y. Contractive auto-encoders: Explicit invariance during feature extraction. InProceedings of the 28th International Conference on Machine Learning (ICML-11) 2011 Jun 28 (pp. 833-840).

Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A. Going deeper with convolutions. InProceedings of the IEEE conference on computer vision and pattern recognition 2015 (pp. 1-9).

He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. InProceedings of the IEEE conference on computer vision and pattern recognition 2016 (pp. 770-778).

Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser Ł, Polosukhin I. Attention is all you need. Advances in neural information processing systems. 2017;30.

Radford A, Narasimhan K, Salimans T, Sutskever I. Improving language understanding by generative pre-training. OpenAI. 2018 Jun 11. Available from: https://openai.com/research/language-understanding

Brown T, Mann B, Ryder N, Subbiah M, Kaplan JD, Dhariwal P, Neelakantan A, Shyam P, Sastry G, Askell A, Agarwal S. Language models are few-shot learners. Advances in neural information processing systems. 2020;33:1877-1901.

Dosovitskiy A, Beyer L, Kolesnikov A, Weissenborn D, Zhai X, Unterthiner T, Dehghani M, Minderer M, Heigold G, Gelly S, Uszkoreit J. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929. 2020 Oct 22. Available from: https://arxiv.org/abs/2010.11929